説明
[高速フーリエ変換]

Fast Image Engene の高速フーリエ変換関数群(以下FIE_FFTと呼称)は、前方／後方の両方の高速フーリエ変換を１次元、２次元において、複素数、実数の両データ形式で行うことが出来ます。

データの型

下記の４種類のデータ型がFIE_FFTでは使用できます。

unsigned char
unsigned short
short
double

FIE_FFTで使用できる複素数データはすべて double型の集合です。下記の３種の形式が利用可能です。

interleaved format
splitted format
packed format

参照:: f_fft_data_type

一次元フーリエ変換とその逆変換

１次元における長さ

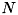の複素数データ

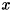の時間領域における順方向フーリエ変換は下式にて定義されます。

$X_k = \sum_{n=0}^{N-1} x_n e^{- \frac {2\pi i } { N } nk } \qquad k = 0,\dots,N-1 \qquad i^2 = -1$

逆フーリエ変換は下式にて定義されます。

$x_k = \sum_{n=0}^{N-1} X_n e^{ \frac {2\pi i }{N} nk } \qquad k = 0,\dots,N-1 \qquad i^2 = -1$

１次元の実数データは、すべての虚数部を０にした複素数データとして処理できます。したがって、複素数データでの定義は実数のデータにも適用することが出来ます。実際には実数データの変換はより効率的に行えるアルゴリズムが実装されています。

二次元フーリエ変換とその逆変換

幅 N 、高さ M の２次元データの順方法フーリエ変換は下式にて定義されます。

$X_{k_1, k_2} = \sum_{n=0}^{N-1} e^{-{2\pi i \over N} nk_1 } \sum_{m=0}^{M-1} e^{-{2 \pi i \over M} mk_2 } x_{n,m} \qquad k_1 = 0,\dots,N-1, \qquad k_2 = 0, \dots, M-1 \qquad i^2 = -1$

２次元データの周波数領域における逆変換は下式にて定義されます。

$x_{k_1, k_2} = \sum_{n=0}^{N-1} e^{ {2\pi i \over N} nk_1 } \sum_{m=0}^{M-1} e^{ {2 \pi i \over M} mk_2 } X_{n,m} \qquad k_1 = 0,\dots,N-1, \qquad k_2 = 0, \dots, M-1 \qquad i^2 = -1$

FIE_FFTで使用できる複素数の２次元データの形式は f_fft_data_type に記述されています。

実際には、２次元のフーリエ変換は、各行に対して１次元のフーリエ変換を行った後、各列に対して１次元のフーリエ変換を行うことで実行されます。２次元の実数データの変換は、虚数部を０にした２次元複素数データの変換を考えることで概念が分かりますが、実際にFIE_FFTに実装されているアルゴリズムは、より効率的に変換を行うようにデザインされています。

フーリエ変換の正規化

フーリエ変換されたデータの値は、データの長さに比例します。そのため、変換結果はデータの長さに応じて正規化する必要があります。 FIE_FFTでは、４種類の正規化手法 (f_fft_normalize_type) が使用可能です。 FIE_FFTの初期化関数を実行する際に、どの手法を使用するかフラグで指定して下さい。周波数画像の可視化が目的の場合はF_FFT_DIV_FWD_BY_Nを、周波数フィルタリングが目的の場合はF_FFT_DIV_INV_BY_Nの利用を推奨します。

参照:: f_fft_normalize_type, fnFIE_fft_1D_alloc(), fnFIE_fft_2D_alloc()

スケーリングとサチュレーション

FIE_FFTでは変換前の空間/時間領域のデータに３種の整数データ形式が使用可能です。変換後の周波数空間データは必ず double 型にて格納されます。したがって、整数データ型への逆フーリエ変換を行う際は、スケール値と飽和処理について考慮する必要があります。 FIE_FFTの整数データ型への逆フーリエ変換関数では、スケーリングと飽和処理を行います。飽和処理は自動で行われますが、スケール値はユーザーが正しく設定しなければ、データのダイナミックレンジをそこなうことになります。

データのサイズ

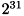FIE_FFTで扱うことが出来る１次元データの長さは $2^{31}$ までです。
２次元画像においても、幅、または高さの最大値は 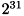$2^{31}$ ですが、実用的な画像サイズはこの制限よりもとても小さくなります。幅、または高さの最小値は 2 です。また、画像の幅及び高さはどちらも2のべき乗の値でなければなりません。

FIE_FFTでフーリエ変換を行うには、どのような形式であってもFIE_FFTハンドルの初期化が必要になります。初期化時に回転因子のテーブルや変換に必要なバッファの確保と初期化が行われ、ハンドルによって管理されます。１次元の変換では、回転因子テーブルの大きさは、変換するデータの長さにより決定されます。２次元の変換では、画像の幅と高さのうち大きな方の値により決定されます。確保されたFFTハンドルは下記の条件がすべて満たされている場合、初期化時に指定したFFT処理とは異なるFFT処理にも使用することが出来ます。

必要な回転因子テーブルの長さが、ハンドルに保持されているテーブルの長さを超えていない。
必要なバッファサイズが、ハンドルによって保持されているサイズを超えていない。

fnFIE_fft_check_spec() 関数を使用すると、確保済みFFTハンドルが目的の処理に使用可能かどうかを確認することが出来ます。 FFTハンドルを初期化時とは異なるFFT処理に使用する場合は、正規化手法の指定に十分注意してください。正規化手法の指定を間違えると、出力結果は間違った物になってしまいます。 fnFIE_fft_get_spec() 関数を使用すると、確保済みFFTハンドルがどの正規化手法を用いるよう設定されているかを確認することが出来ます。

関数名命名則

FIE_FFTには沢山の関数があるため、理解しやすいようにFIE_FFTの関数名命名則を示します。 FIE_FFTの関数名命名則は次のようになっています。

接頭語
FIE_FFTでは２種類の接頭語が使われます。
fnFIE_fft_ は１次元の変換関数を示します。
fnFIE_fft2_ は２次元の変換関数を示します。
変換方向
順方向変換は _fwd_ で示されます。
逆方向変換は _inv_ で示されます。
入力データ型
上記で記述したとおり、FIE_FFTでは４種の実数データ型と、３種の複素数データ型が使用できます。これらのデータ型は下記のように表記されます。
- C: interleaved complex 1D or 2D data
- DD: splitted complex 1D or 2D data
- Pack: packed complex 1D data
- UC8: unsigned char type of real 1D data
- US16: unsigned short type of real 1D data
- S16: short type of real 1D dat
- D64: double type of real 1D data
- Real: 2D data of real type including F_IMG_UC8, F_IMG_S16, F_IMG_US16 and F_IMG_DOUBLE.
出力データ型出力データ型の表記は入力データ型の表記法と同じです。
出力データ先メモリ
_in は出力データが入力データと同じメモリに格納される関数を示します。
_out は出力データが入力データとは別のメモリに格納される関数を示します。
関数名に _in 又は _out を含まない関数は _out の動作と同じです。

2次元FFT後の画像(周波数領域画像)について

fnFIE_fft2_fwd_RealtoDD() によって実画像を周波数領域画像へ変換できます。出力される画像は、浮動小数点画像(F_IMG_DOUBLE)となっています。変換した画像から fnFIE_fft2_get_mag_and_phase_DD() を用いて強度画像（振幅スペクトル画像）と角度画像（位相スペクトル画像）を得ることもできます。周波数画像は画像の四方の角から低周波成分、中央に近づくに従って高周波成分となります。また、画像の左上1画素は直流成分を表します。

周波数画像例

入力画像

強度画像

強度画像は2のべきサイズになるようにリサイズされた入力画像から生成しています。右の図は強度画像をUC8の濃淡画像(F_IMG_UC8, 1ch)に変換して可視化したものです。

サンプルコード: 周波数画像可視化サンプル
 FFTを使用した実画像の周波数フィルタリングのサンプル

参考文献:

Eleanor Chu and Alan George, "INSIDE the FFT BLACK BOX: Serial and Parallel Fast Fourier Transform Algorithms", Ch.14, 2000, CRC Press
Duhamel,P. ^ Vetterli M. "Fast Fourier Transforms: ATutorial Review and a State of the Art" Digital Signal Processing Handbook Ed.Vijay K. Madisetti and Douglas B. Williams Boca Raton: CRC Press LLC, 1999
画像情報教育振興協会, "ディジタル画像処理[改訂新版]," pp.126-128, 2015.

説明 [高速フーリエ変換]

説明
[高速フーリエ変換]