説明
[ナイーブベイズ分類器]
ナイーブベイズ分類器について
ナイーブベイズ分類器は確率モデルに基づいた、単純ながら強力な識別器モデルです。 ナイーブベイズ分類器で構築される識別器の概念図を以下に示します。
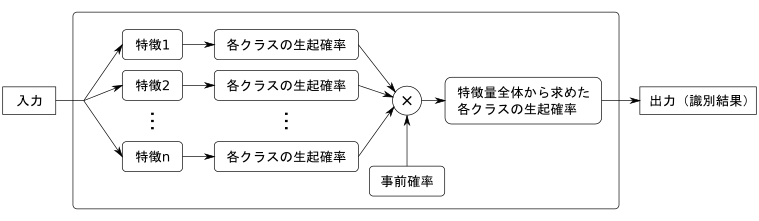
ナイーブベイズ分類器は、特徴量を要素ごと独立に出力が得られる確率を計算します。 その後得られた確率すべての積を取ることで統合し、確率が最大となるクラスを識別結果として出力します。 特徴量の独立性の仮定により学習と識別を単純に実行できることが、ナイーブベイズ分類器の利点となります。
ナイーブベイズ分類器の原理
ナイーブベイズ分類器はベイズの定理と単純な条件付独立の仮定に基づき、確率モデルを用いて多クラスの識別問題を解きます。
入力特徴ベクトル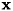 から出力のラベル
から出力のラベル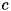 を求める識別問題を考えます。 このとき、入力
を求める識別問題を考えます。 このとき、入力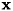 が与えられたときに出力が
が与えられたときに出力が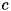 になる確率は、確率変数X, Cを用いて
になる確率は、確率変数X, Cを用いて 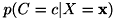 と表記されます。
と表記されます。
このような識別問題の具体例としては、気温や湿度、風向から天気を求める問題(Xは{気温, 湿度, 風向}の3種類からなり、Cは{晴れ, 曇り, 雨, 雪}の4種類をとる)や、ワークの二値ブローブから外観検査を行う問題(Xは二値ブローブ特徴量からなり、Cは{良品, 欠品}の2種類をとる)が挙げられます。
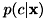 が最大になるラベル
が最大になるラベル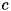 を求めることで識別問題を解くことができます。 しかし、ほとんどの場合
を求めることで識別問題を解くことができます。 しかし、ほとんどの場合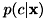 は直接求められません。 そこで、ベイズの定理により
は直接求められません。 そこで、ベイズの定理により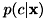 を次のように変形します。
を次のように変形します。
![\[ p(c|{\bf x})=\frac{ p({\bf x}|c)p(c) }{ p({\bf x}) } \]](form_444.png)
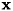 は入力として与えられるので、
は入力として与えられるので、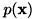 は定数とみなせます。すると
は定数とみなせます。すると
![\[ p(c|{\bf x}) \propto p({\bf x}|c)p(c) \]](form_446.png)
となります。この右辺を最大化することで識別問題を解くことができます。
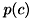 は事前確率と呼ばれ、
は事前確率と呼ばれ、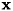 がわからないときの
がわからないときの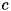 の出現確率を表します。 一様であることを仮定したり、教師データのクラス数比率などにより推定されます。
の出現確率を表します。 一様であることを仮定したり、教師データのクラス数比率などにより推定されます。
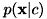 は尤度と呼ばれます。 尤度は特徴ベクトルを要素ごとに
は尤度と呼ばれます。 尤度は特徴ベクトルを要素ごとに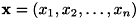 と置くことでさらに分解され、
と置くことでさらに分解され、 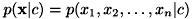 と表現できます。 ここで、「特徴ベクトルの各次元同士は全く相関がない」という強い仮定(ナイーブな仮定)を置きます。 すると、ベイズの定理を繰り返し適用することにより、
と表現できます。 ここで、「特徴ベクトルの各次元同士は全く相関がない」という強い仮定(ナイーブな仮定)を置きます。 すると、ベイズの定理を繰り返し適用することにより、
![\[ p(x_1, x_2, \dots, x_n|c) = p(x_1|c) p(x_2|c) \dots p(x_n|c) = \prod_{i=1}^n p(x_i|c) \]](form_451.png)
と変形できます。 この結果、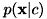 が要素ごとに独立に
が要素ごとに独立に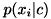 を求めて積を取ることで求まるので、算出が容易になります。
を求めて積を取ることで求まるので、算出が容易になります。
この強い仮定は、多くの場合、実際に観測される事象と反しています。 例えば画像の画素値集合を特徴ベクトルとしたとき、「隣接する画素の画素値は多くの場合よく似ている」という情報を無視することになります。 しかしながら、単純な独立性仮定のもとでも性能の高い識別結果を得られることが知られています。
カテゴリ属性と数値属性の扱い
ナイーブベイズ分類器では、入力の特徴ベクトルの属性として、「数値属性」と「カテゴリ属性」を扱うことができます。
数値属性とは、特徴ベクトルの各値が連続変数、つまり2つの異なる値が数値として比較可能なものであることを意味します。 例として、"画素の濃度"や"対象物の面積"のように、具体的に数値として観測されたものが当たります。
カテゴリ属性とは、特徴ベクトルの各値が、離散的なクラスラベルを示す値であることを意味します。 例として「矩形 = 0」「円 = 1」「楕円 = 2」のように、特定の属性を数値と対応させ、その属性を示す ラベルとしたものが当たります。
なお、カテゴリ属性のベクトルを扱う場合、特徴ベクトルの各値は全て整数値である必要があります。
尤度の確率分布モデル
特徴ごとの尤度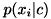 は適当な確率分布でモデル化されます。 本ライブラリでは次の3種類をサポートします。
は適当な確率分布でモデル化されます。 本ライブラリでは次の3種類をサポートします。
- 正規分布
- 数値属性の特徴ベクトルを用いる分布です。 次の式で表されます。
![\[ p(x_i|c) \propto \exp \left( - \frac{(x_i - \mu_i)^2}{2 \sigma_i^2} \right) \]](form_453.png)
ここで、
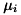 ,
, 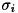 はそれぞれ分布の平均と標準偏差を表します。 特徴量に任意の実数を取ることができるため、様々な教師データに適用できる分布です。
はそれぞれ分布の平均と標準偏差を表します。 特徴量に任意の実数を取ることができるため、様々な教師データに適用できる分布です。
- 多変量多項分布
- カテゴリ属性の特徴ベクトルを用いる分布です。 次の式で表されます。
![\[ p(x_i|c) = \begin{cases} p_{i,j} & (x_i = j, \ j = 1 \dots m_i) \\ 0 & (\text{otherwise}) \end{cases} \]](form_456.png)
ここで、
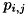 は、
は、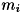 種類の値を取るカテゴリ属性の変数
種類の値を取るカテゴリ属性の変数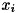 について、
について、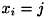 となる確率を表します (
となる確率を表します (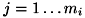 ,
, 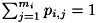 )。 簡単のため、ここでは
)。 簡単のため、ここでは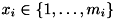 であるとします。実際は
であるとします。実際は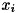 は任意の整数値をとることができます。
は任意の整数値をとることができます。
- 多項分布
- ヒストグラムを特徴ベクトルとして用いる分布です。 ヒストグラムでは特徴ベクトルの各要素
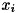 が頻度を表します。 頻度とは、例えば文書分類において文書内にある単語が出現する回数のような、個数のカウントのことを表します。 次の式で表されます。
が頻度を表します。 頻度とは、例えば文書分類において文書内にある単語が出現する回数のような、個数のカウントのことを表します。 次の式で表されます。 ![\[ p(x_i|c) \propto p_i^{x_i} \]](form_464.png)
ここで、
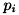 はi番目のデータがn個の要素の中から現れる確率を表します(
はi番目のデータがn個の要素の中から現れる確率を表します(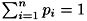 )。 実用上は、頻度は重み付きでもよいため、非負の実数をとるヒストグラムを特徴量として使用することができます。 スパムメール判定などの文書分類で高い性能をもつことが知られています。 なお、多項分布となるのは尤度
)。 実用上は、頻度は重み付きでもよいため、非負の実数をとるヒストグラムを特徴量として使用することができます。 スパムメール判定などの文書分類で高い性能をもつことが知られています。 なお、多項分布となるのは尤度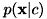 であり、上記の式は厳密な多項分布モデルではありません。
であり、上記の式は厳密な多項分布モデルではありません。
ナイーブベイズ分類器の学習
学習は特徴ごとの尤度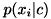 の分布パラメータを最尤推定により求めることで行われます。 実際には、後述の特徴量が一定値になる場合の対策も同時に適応されます。
の分布パラメータを最尤推定により求めることで行われます。 実際には、後述の特徴量が一定値になる場合の対策も同時に適応されます。
- 正規分布
- 平均
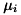 と標準偏差
と標準偏差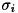 を推定します。 ラベルがcとなる教師データの特徴量
を推定します。 ラベルがcとなる教師データの特徴量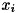 の平均と標準偏差が用いられます。
の平均と標準偏差が用いられます。
- 多変量多項分布
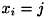 となる確率
となる確率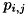 を推定します。 ラベルがcとなる教師データのうち、
を推定します。 ラベルがcとなる教師データのうち、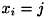 を満たすデータの個数がラベルcの全データの個数に占める割合として推定されます。
を満たすデータの個数がラベルcの全データの個数に占める割合として推定されます。
- 多項分布
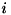 番目のデータが出現する確率
番目のデータが出現する確率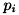 を推定します。 ラベルがcとなる教師データのうち、
を推定します。 ラベルがcとなる教師データのうち、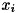 の総和が全頻度の総和に占める割合として推定されます。
の総和が全頻度の総和に占める割合として推定されます。
特徴量が一定値になる場合の対策
教師データにおいて特徴量のある要素が一定値であった場合、学習されたナイーブベイズ分類器が出力する確率値は常に0となってしまいます。 これは「ゼロ頻度問題」として広く知られているナイーブベイズ分類器の問題です。この問題を回避するため、次の対策を行っています。
- 正規分布: 一様分布を仮定し、一定値となった特徴要素を無視します。
- 多変量多項分布、多項分布: スムージングと呼ばれる処理を適用します。実際に得られた頻度に対し、αだけ多く個数をカウントします。αは0以上の実数であり、パラメータとして指定されるものです。
ナイーブベイズ分類器のパラメータ
ナイーブベイズ分類器で必要となるパラメータを説明します。精度の高い識別を行うためには、パラメータの調整が必要です。
- 尤度のタイプ
- 学習で用いる尤度のタイプを設定します。
- F_ML_NB_GAUSSIAN : 正規分布。特徴ベクトルは数値属性である必要があります。
- F_ML_NB_MULTINOMIAL_MULTIVARIATE : 多変量多項分布。特徴ベクトルはカテゴリ属性である必要があります。
- F_ML_NB_MULTINOMIAL : 多項分布。特徴ベクトルは非負の実数であるヒストグラムである必要があります。
- 事前分布のタイプ
- 学習で用いる事前分布のタイプを設定します。
- F_ML_NB_PRIOR_UNIFORM : 一様分布を仮定します。
- F_ML_NB_PRIOR_PROPORTION : クラスごとの教師データ数の比率により推定します。クラスごとの教師データ数の偏りが実際のデータに即している場合に使用すると良いでしょう。
- スムージング係数α
- ゼロ頻度問題に対処するためのパラメータです。 尤度として多変量多項分布または多項分布を指定した場合に使用されます。 0以上の実数を設定可能であり、1の場合はラプラススムージングと呼ばれ、多くの場合このラプラススムージングを指定することが推奨されます。 なお、0を指定した場合はスムージングなしとなります。
- 事前処理
- 学習を開始する前に、与えられた教師データに行う前処理を指定します。 指定可能な事前処理は以下のものになり、これらは組み合わせて同時に指定可能です。
- 重複した教師データの削除
入力された教師データの中で、特徴量がまったく同じデータが複数存在したときに、以下のルールに従って データを削除します。- 同一クラス内の重複データ :クラス内に一つだけ残るようにして、他を全て削除します。
- 複数クラス間での重複データ:「矛盾データ」と判断して、全て削除します。
- データの正規化
教師データとして与えられた特徴ベクトルの各成分ごとの最大値・最小値を探索し、その値で 全ての特徴ベクトルを一定の範囲に正規化します。入力される特徴ベクトルが極めて小さい場合など、 数値計算上の誤差が考えられる場合、正規化を行うことで、これを回避するなどの効果が期待できます。
値の範囲は、尤度が正規分布である場合は [-1.0, 1.0] とし、多項分布である場合は [0.0, 1.0] となります。
なお、尤度が正規分布である場合は、内部的に平均と標準偏差が利用されるため、データの正規化はほとんど意味を持ちません。データの正規化以外のパラメータ調整を行うことを推奨します。
- 教師データの特徴ベクトルがカテゴリ属性で合った場合は、事前処理の指定は無視されます。これは以下の理由によります
- 特徴ベクトルの値は属性を示すラベルを意味し、数値的な意味を持たない
- カテゴリ属性の場合は、重複性は分岐を決定する上でむしろ情報となるため
- また、ナイーブベイズ分類器の学習では、まずは事前処理を指定せずに学習を行い、パラメータの調整で精度を上げていく事を推奨します。
- 学習時間
- 学習を行う時間の上限を秒単位で設定します。教師データの内容や、パラメータ の指定によっては、学習に極端に時間がかかる場合があります。このパラメータで学習に用いる時間の 上限を設定しておくと、学習の終了条件を満たす前であっても学習を打ち切ります。 値を0にすると、終了条件を満たすまで学習を続ける設定になります。
その他
- ナイーブベイズ分類器の利点
- 学習が高速で、識別も比較的高速
使用する尤度モデルに依りますが、学習は他の識別器と比べて非常に高速となります。識別も高速に動作します。 - 比較的少ない教師データ数でも精度のよい学習ができる
識別のルールが単純であるため、多くの場合で学習に大量のデータを必要としません。 - 過学習を起こしにくい
単純な確率モデルを使用しているため、教師データに対して過剰なフィッティングを起こしにくいという特徴があります。 - 高次元のデータに強い
特徴間の相関を考慮しないため、「次元の呪い」と呼ばれるような高次元の問題を緩和できます。
- ナイーブベイズ分類器の欠点
- クラス間・特徴量間の相関を考慮しないため、強い相関があると著しく性能が落ちる
画素値をそのまま特徴量とした場合のように、強い相関のある特徴量に対してはナイーブベイズは低い性能を示すことが予想されます。
この問題を解決するには、特徴量の相関がなくすような処理を加えることや、他の特徴量、他の機械学習を用いることが考えられます。
- 参考文献:
- [1]元田 浩・山口 高平・津本 周作・沼尾 正行. データマイニングの基礎. オーム社. 2006. pp.35-39
- [2]Sebastian Raschka. Naive Bayes and Text Classification I - Introduction and Theory. CoRR. abs/1410.5329. 2014.