説明
[サポートベクターマシン]
サポートベクターマシンについて
サポートベクターマシン(SVM)は、V.Vapnikらが発表した、2クラス識別の教師あり学習アルゴリズムです。 この学習アルゴリズムは
- 「マージン最大化」による未学習データに対する高い汎化能力
- カーネル関数を用いることによる、非線形分離への対応
SVMの概念図を以下に示します。
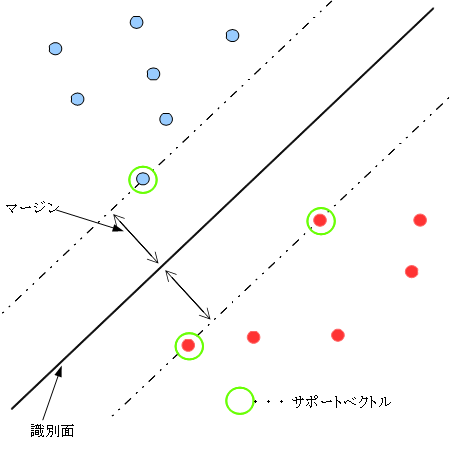
教師データを基にしてクラスを識別することは、与えられた教師データを分類するような識別面を求めること ともいえます。識別面が決定すれば、未知のデータが入力されたときに、それが識別面のどちら側になるかで クラスを予測することができます。しかし、このような識別面は一般に無数に存在します。
サポートベクターマシンは、与えられた教師データと識別面までの最短距離(マージン)を最大化 するような線形な識別面を選択します(マージン最大化)。
これは、与えられた教師データのグループの間のちょうど真ん中に識別面を引くことに相当します。 また、この識別面に最も近い位置に存在する教師データは、この識別面を決定付けるものであり、 これらは「サポートベクトル」と呼ばれます。
「マージンが最大となる」「クラス間に線形な識別面が設定できる」ようなSVMを「ハードマージンSVM」といいます
重なりのあるクラス分類
ハードマージンSVMでは、教師データ群が線形の識別面で完全に分離可能であることを仮定してい ます。一般的な分類問題では、教師データのオーバーラップがあるなど、厳密な線形分離をすることが できないものも多数あります。そのため、SVMでは「マージンが最大となる」という制約条件を緩和し、 教師データが境界の「間違った側」に存在することを許容する(ただし、そのようなデータにはペナルティを与える)ことで、 この問題に対応しています。つまり、一部の教師データの誤識別を許容するようにしつつ、線形な識別面を 選択することになります。このようなSVMを「ソフトマージンSVM」といいます。ソフトマージンSVMの概念図を以下に示します。
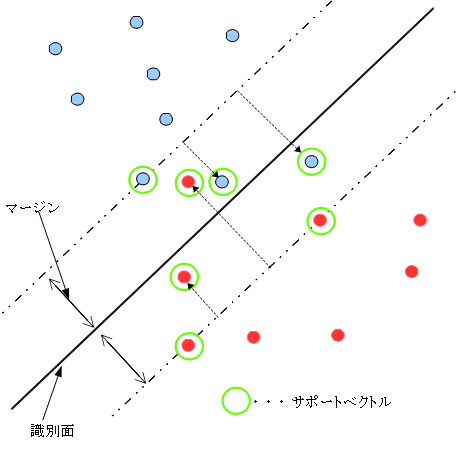
上記の図では、いくつかの教師データがマージンの内部、もしくは識別面を超えた位置に存在し ています。このようなデータの存在を許容しつつ(ただしペナルティを与える)マージン最大化を 図っています。
どの程度誤識別が許容されるかは、ユーザがパラメータにて指定します。
非線形分離への対応
SVMでは、通常2つのクラスを線形で分離することを目的としています。しかし、教師データの入力空間上で そもそも線形分離可能ではないようなケースも存在します。 このような状況では、たとえマージンが最大となるような識別面を求めたとしても、 性能のよい識別はできません。すなわち、このような問題に対しては、空間内で非線形分離を行う必要があります。
この問題を解決するために、SVMでは入力空間をより高次元の「特徴空間」と呼ばれる内積空間 へ写像し、その空間上でマージンが最大化するように識別面を決定する方法が考案されています。 高次元の空間へ写像することで、クラス間の線形分離性を向上させ、その上で分離を行うというものです。
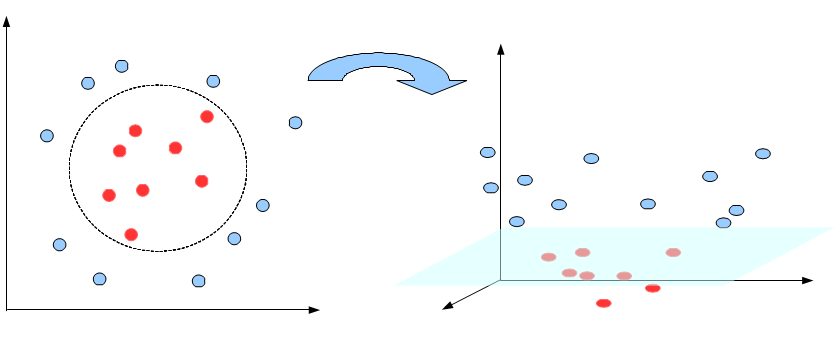
しかし、高次元空間への写像を明示的に定義し、陽に特徴空間の変換とベクトル演算を行うこと は大変困難な問題になります。そのため、SVMでは「カーネル関数」を用いることで、この問題を解決しています。 ここではカーネル関数の詳細については触れませんが、このカーネル関数を用いることで、高次元への 空間写像を明示的に求めることなく、高次元空間上での内積を求めることができます(これをカーネル・トリックといいます)。 この方法により、SVMは元の入力空間では非線形分離が必要となるような識別にも対応が可能となってます。
カーネル関数は様々なものが提案されており、用いるカーネル関数によって、入力空間がどのような 高次元空間に写像されるかが決まります。問題に応じて適切なカーネル関数とそのパラメータを選択することで、 識別能力を向上させることができます(これがSVMの特徴の一つでもあります)。
SVMのパラメータ
SVMにおいて必要となるパラメータを説明します。SVMは優れた識別能力をもつ学習アルゴリズム ですが、より良い識別結果を出すためには、パラメータやモデルの適切な選択・調整が必要になります。
- SVMのタイプ
- SVMには、多数の拡張されたモデルが存在します。本ライブラリでは、現在以下のものについて対応しています。
- C-SVM : 教師データの誤分類に対するペナルティパラメータを持つ、多クラス識別SVM。標準的なSVMモデル
- マージンパラメータ
- ソフトマージンにおける誤分類の許容パラメータです。指定するSVMのSVMのタイプによってパラ メータのもつ意味が異なってきます。
- C-SVM : 0よりも大きな値をとる、誤分類に対するペナルティパラメータです。値を大きくするほど、 ハードマージンとなります。最適値は学習対象などによって異なりますが、ディフォルトでは1.0程度を 指定するとよいでしょう。
- 学習の停止条件
- 学習の停止基準値。ここでは最適化問題を解く際の、解の収束判定値です。値を大きくすると 学習時間が短縮されますが、その分学習精度が落ちます。ディフォルトでは0.001程度になります。
- カーネル関数
- SVMで用いるカーネル関数の適切な指定とパラメータの設定は、SVMの能力を引き出す上で最も 重要な要素です。本ライブラリでは以下のカーネル関数に対応しています。 また、カーネル関数に付随するパラメータについても、あわせて説明します。
- 線形カーネル
以下の式で与えられるカーネル関数です。
![\[ K( {\bf x_{1}},{\bf x_{2}}) = {\bf x_{1}} \cdot {\bf x_{2}} \]](form_467.png)
- これは単純な内積であり、高次元への写像は行われません。もとの入力空間内で線形分離が行われます。 入力空間が元々高次元であり(つまり学習する特徴量の種類が多い場合)、データ分布が疎である場合によく用いられます。
このカーネルにおいて、ユーザが指定すべきパラメータはありません。
- 多項式カーネル
以下の式で与えられるカーネル関数です。
![\[ K( {\bf x_{1}},{\bf x_{2}}) = (\gamma ({\bf x_{1}} \cdot {\bf x_{2}}) + c)^d \]](form_468.png)
- このカーネル関数で決まる写像は、高次元
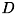 への写像となります。入力空間の次元が
への写像となります。入力空間の次元が 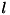 であるとき、次元
であるとき、次元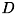 の次元数は
の次元数は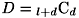 となります。 また、
となります。 また、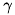 は内積に対するスカラー、
は内積に対するスカラー、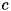 は低次の項の影響力を調整する0次の係数に なります。特に離散的な特徴の識別に対して用いられるカーネルです。
は低次の項の影響力を調整する0次の係数に なります。特に離散的な特徴の識別に対して用いられるカーネルです。
カーネルの次数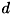 , スカラー
, スカラー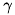 , 0次係数
, 0次係数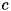 は、ユーザが指定する必要があります。
は、ユーザが指定する必要があります。
- 動径基底関数カーネル(RBFカーネル)
以下の式で与えられるカーネル関数です。
![\[ K( {\bf x_{1}},{\bf x_{2}}) = \exp(- \gamma \|{\bf x_{1}} - {\bf x_{2}}\|^2 ) \]](form_474.png)
- このカーネル関数では、入力空間は無限次元へ写像されます。データやその分布に対して 事前知識がない場合に用いられる汎用的なカーネルであり、最もよく用いられるカーネルの一つです。
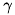 はサポートベクトルが識別に及ぼす空間の範囲(分散)を決定するパラメータです。
はサポートベクトルが識別に及ぼす空間の範囲(分散)を決定するパラメータです。 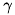 を小さくすると、より大局的な範囲に影響を与えるようになり、逆に大きくすると局所的な範囲と なります。そのため、一般的には
を小さくすると、より大局的な範囲に影響を与えるようになり、逆に大きくすると局所的な範囲と なります。そのため、一般的には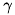 が大きくなるほど、サポートベクトルの数が増え、より複雑な 識別面を構成するようになりますが、過学習(オーバーフィッティング)を起こしやすくなります。
が大きくなるほど、サポートベクトルの数が増え、より複雑な 識別面を構成するようになりますが、過学習(オーバーフィッティング)を起こしやすくなります。
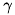 は、ユーザが指定する必要があります。
は、ユーザが指定する必要があります。
- 事前処理
- 学習を開始する前に、与えられた教師データに行う前処理を指定します。 前処理を適切に行うことで、学習時間の短縮や、識別精度の向上が期待できます。 指定可能な事前処理は以下のものになり、これらは組み合わせて同時に指定可能です。
- 重複した教師データの削除
入力された教師データの中で、特徴量がまったく同じデータが複数存在したときに、以下のルールに従って データを削除します。- 同一クラス内の重複データ :クラス内に一つだけ残るようにして、他を全て削除します。
- 複数クラス間での重複データ:「矛盾データ」と判断して、全て削除します。
- データの正規化
教師データとして与えられた特徴ベクトルの各成分ごとの最大値・最小値を探索し、その値で 全ての特徴ベクトルを [-1.0, 1.0] の範囲に正規化します。これにより「値の取りうる範囲の大き い成分が支配的になる問題を解消する」「数値計算上の情報落ちを防ぐ」「学習時間の短縮」が 期待できます。
SVMにおいては、この事前処理を行うことが推奨されます。
- 学習時間
- 学習を行う時間の上限を秒単位で設定します。教師データの内容や、パラメータ、カーネル関数 の指定によっては、学習に極端に時間がかかる場合があります。このパラメータで学習に用いる時間の 上限を設定しておくと、学習の終了条件を満たす前であっても学習を打ち切ります。 値を0にすると、終了条件を満たすまで学習を続ける設定になります。
その他
- 多クラス対応について:
- SVMは、本来は2クラス識別の学習アルゴリズムであり、3クラス以上の多クラス識別に 対応したものではありません。本ライブラリでは、多クラス識別への対応として、 「1対1(one-versus-one)方式」を用いています(「ペアワイズ(pairwise)方式」とも呼ばれています)。 これは、N個のクラス識別に対して、異なる二つのクラスのあらゆるペアを作り、 そのペア毎にSVMを適応するというものです。(そのため、内部的には、2クラス識別器が全部で N(N-1)/2個作成されます )
識別を行う際には、このN(N-1)/2個の識別器ごとに識別を行い、その多数決で識別を行います。
- モデル選択・パラメータの調整について:
- SVMで識別性能を引き出すためには、モデル選択やパラメータの調整が必要になります。しかし、 これらを一意的に決定するような方法は、現在のところ存在しません。そのため、ある程度実験 的な評価を繰り返しながら、調整をしていく必要があります。
基本的な指針として、以下のことを検討してみると良いでしょう。
- カーネル関数は動径基底関数カーネルを選択する
動径基底関数カーネルは汎用的なカーネルであり、大抵の識別問題に対して適しています。
- パラメータは小さな値から始め、識別率の向上が見受けられる間は値を上げていく
最初は制約条件を緩くして、識別率の向上が見られる間は制約を厳しくしていき、効率的に、かつ 網羅的にパラメータの組み合わせを見つけていきます。
また、最初はパラメータの刻みを大雑把にして(例: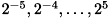 のように指数的に増やす)、 識別率が高くなる組み合わせの範囲をある程度限定してから、細かくパラメータをチェックすると良いでしょう
のように指数的に増やす)、 識別率が高くなる組み合わせの範囲をある程度限定してから、細かくパラメータをチェックすると良いでしょう
- 参考文献:
- [1]C.M.ビショップ. パターン認識と機械学習 -ベイズ理論による統計的予測(下). 元田 浩 他 監訳 . 丸善出版. 2008. 433p
- [2]Nello Cristinini et al., サポートベクターマシン入門. 大北 剛 訳. 共立出版. 2005. 252p
- [3]阿部 重夫. パターン認識のためのサポートベクトルマシン入門. 森北出版. 2011. 224p
- [4]前田 英作. "カーネル情報処理入門 -非線形の魅惑-". コンピュータビジョン最先端ガイド2. 八木 康史 他 編著. アドコムメディア株式会社. 2010. p.91-132