基本理論
[カメラキャリブレーション]
ピンホールカメラモデル
同次座標を用いて2次元座標上の点を![$ \tilde{\bf{m}} = \left[ \begin{array}{ccc} u & v & 1 \end{array} \right]^t $](form_1075.png) 3次元座標上の点を
3次元座標上の点を ![$ \tilde{\bf{M}} = \left[ \begin{array}{cccc} X& Y& Z& 1 \end{array} \right]^t $](form_1076.png) と表します。 この同次座標を用いると、ピンホールカメラモデルでの 3Dワールド座標点から画像の2D座標点(撮像平面) への座標変換は次式にて表現できます。
と表します。 この同次座標を用いると、ピンホールカメラモデルでの 3Dワールド座標点から画像の2D座標点(撮像平面) への座標変換は次式にて表現できます。
![\[ s\tilde{\bf{m}} = \bf{A}\ [\bf{R}|\bf{T}]\ \tilde{\bf{M}} \]](form_1077.png)
ただし、
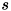 : 任意の定数
: 任意の定数
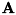 :カメラ内部パラメータ行列
:カメラ内部パラメータ行列
![$[\bf{R}|\bf{T}]$](form_1079.png) :3Dカメラ外部パラメータ行列
:3Dカメラ外部パラメータ行列
カメラ内部パラメータ行列 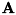 は正規化カメラ座標系から理想画像座標系への変換を表し、 次のように定義されます。
は正規化カメラ座標系から理想画像座標系への変換を表し、 次のように定義されます。
![\[ \bf{A} = \left[ \begin{array}{ccc} \alpha & \gamma & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \\ \end{array} \right] \]](form_1067.png)
ただし
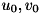 :画像上の光軸中心(主点)へのオフセット成分
:画像上の光軸中心(主点)へのオフセット成分
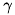 :スキュー成分
:スキュー成分
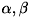 :スケール成分
:スケール成分
3Dカメラ外部パラメータ行列 ![$[\bf{R} | \bf{T}]$](form_1082.png) は、 3x3の回転行列
は、 3x3の回転行列 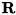 と 1x3の並進行列
と 1x3の並進行列 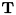 を結合したもので、 ワールド座標系と正規化カメラ座標系の間の変換を表します。 各成分による表記をすれば、
を結合したもので、 ワールド座標系と正規化カメラ座標系の間の変換を表します。 各成分による表記をすれば、
![\[ \left[ \bf{R} | \bf{T} \right] = \left[ \begin{array}{cccc} r_{11} & r_{12} & r_{13} & t_1\\ r_{21} & r_{22} & r_{23} & t_2\\ r_{31} & r_{32} & r_{33} & t_3 \end{array} \right] \]](form_1083.png)
となります。
次にキャリブレーションに使用するモデルの座標を考えます。 当ライブラリではモデル点列は平面上に存在していると仮定しており、 その平面上に原点を、平面に直交する方向にZ軸を置きます。 するとこの座標系におけるモデルの3次元座標は、 ![$ \tilde{\bf{M}} = \left[ \begin{array}{cccc} X & Y & 0 & 1 \end{array} \right]^t $](form_1084.png) と書けるので、
と書けるので、
![\[ s\tilde{\bf{m}} = \bf{A} \left[ \begin{array}{cccc} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \end{array} \right] \left[ \begin{array}{c} X\\ Y\\ 0\\ 1 \end{array} \right] \]](form_1085.png)
となります。 Z軸の値が全てゼロになるため、これを書き直すと、
![\[ s\tilde{\bf{m}} = \bf{A} \left[ \begin{array}{ccc} r_{11} & r_{12} & t_1 \\ r_{21} & r_{22} & t_2 \\ r_{31} & r_{32} & t_3 \end{array} \right] \left[ \begin{array}{c} X\\ Y\\ 1 \end{array} \right] \]](form_1086.png)
となります。 本ライブラリでは、この3x3行列
![\[ \bf{Rt} = \left[ \begin{array}{ccc} r_{11} & r_{12} & t_1 \\ r_{21} & r_{22} & t_2 \\ r_{31} & r_{32} & t_3 \end{array} \right] \]](form_1087.png)
を 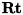 と記述し、単に カメラ外部パラメータ と呼称しています。 この行列は正規化カメラ座標系とワールド空間上のある平面、 つまり、2Dワールド座標との関係を表しています。 また、
と記述し、単に カメラ外部パラメータ と呼称しています。 この行列は正規化カメラ座標系とワールド空間上のある平面、 つまり、2Dワールド座標との関係を表しています。 また、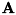 と
と 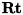 の積によるホモグラフィ行列
の積によるホモグラフィ行列  を
を
![\[ \bf{H} = \bf{A}\ \bf{Rt} \]](form_1088.png)
と定義し、これを 混合カメラパラメータ と呼称することにします。 この行列は理想画像座標系と2Dワールド座標との関係を表しています。
レンズ放射歪み
実際のカメラはピンホールカメラと異なり、光軸からの距離に応じた 放射歪みを伴います。そのため、これをモデル化し補正する必用が有ります。 本ライブラリでは、この放射歪みを次式によりモデル化しています。
![\[ \begin{array}{l} \breve{x} = x+x[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \\ \breve{y} = y+y[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \end{array} \]](form_1089.png)
ただし、
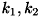 :放射歪み係数
:放射歪み係数
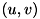 :歪みのない理想的な(観測することができない)画像座標上での点座標
:歪みのない理想的な(観測することができない)画像座標上での点座標
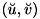 :実際に撮像した、歪みのあるカメラ画像座標上での点座標
:実際に撮像した、歪みのあるカメラ画像座標上での点座標
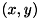 :
: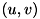 を正規化画像座標系へ変換した座標
を正規化画像座標系へ変換した座標
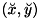 :
: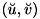 を正規化画像座標系へ変換した座標
を正規化画像座標系へ変換した座標
ここで、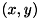 はカメラ内部パラメータ行列の成分を用いて
はカメラ内部パラメータ行列の成分を用いて
![\[ \begin{array}{l} \breve{u} = \alpha\breve{x}+\gamma\breve{y}+u_0 \\ \breve{v} = \beta\breve{y}+v_0 \end{array} \]](form_1094.png)
と書けるので
![\[ \begin{array}{l} \breve{u} = u+(u-u_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \\ \breve{v} = v+(v-v_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \end{array} \]](form_1095.png)
となります。本ライブラリではこの式を用いて理想画像座標系と 歪みのあるカメラ画像座標系(カメラ画像座標系)との変換を行います。