線形代数
[行列演算]
関数 | |
| INT FVALGAPI | fnFIE_mat_inverse (FMATRIX *a) |
| 逆行列の算出 | |
| INT FVALGAPI | fnFIE_mat_solve (FMATRIX *a, FVECTOR *b, FVECTOR *x) |
| 連立一次方程式の計算 | |
| INT FVALGAPI | fnFIE_mat_inverse2 (FMATRIX *a, FMATRIX *a_inv, DOUBLE *det) |
| 逆行列の算出(LU分解採用) | |
| INT FVALGAPI | fnFIE_mat_trans (const FMATRIX *a, FMATRIX *ad) |
| 行列の転置 | |
| INT FVALGAPI | fnFIE_mat_trace (const FMATRIX *a, DOUBLE *trace) |
| 行列のトレースを計算 | |
| INT FVALGAPI | fnFIE_mat_mul_av (const FMATRIX *a, const FVECTOR *vs, FVECTOR *vd) |
| 行列とベクトルのかけ算 | |
| INT FVALGAPI | fnFIE_mat_mul_va (const FVECTOR *vs, const FMATRIX *a, FVECTOR *vd) |
| ベクトルと行列のかけ算 | |
| INT FVALGAPI | fnFIE_mat_mul_aa (const FMATRIX *a1, const FMATRIX *a2, FMATRIX *ad) |
| 行列と行列のかけ算 | |
| INT FVALGAPI | fnFIE_mat_mul_as (const FMATRIX *a, DOUBLE s, FMATRIX *ad) |
| 行列とスカラーのかけ算 | |
| INT FVALGAPI | fnFIE_mat_mul_vs (const FVECTOR *v, DOUBLE s, FVECTOR *vd) |
| ベクトルとスカラーのかけ算 | |
| INT FVALGAPI | fnFIE_mat_sum_aa (const FMATRIX *a1, const FMATRIX *a2, FMATRIX *ad) |
| 行列の足し算 | |
| INT FVALGAPI | fnFIE_mat_sum_vv (const FVECTOR *v1, const FVECTOR *v2, FVECTOR *vd) |
| ベクトルの足し算 | |
| INT FVALGAPI | fnFIE_mat_sum_as (const FMATRIX *a, DOUBLE s, FMATRIX *ad) |
| 行列とスカラーの足し算 | |
| INT FVALGAPI | fnFIE_mat_sum_vs (const FVECTOR *v, DOUBLE s, FVECTOR *vd) |
| ベクトルとスカラーの足し算 | |
| INT FVALGAPI | fnFIE_mat_sub_aa (const FMATRIX *a1, const FMATRIX *a2, FMATRIX *ad) |
| 行列の引き算 | |
| INT FVALGAPI | fnFIE_mat_sub_vv (const FVECTOR *v1, const FVECTOR *v2, FVECTOR *vd) |
| ベクトルの引き算 | |
| INT FVALGAPI | fnFIE_mat_sub_as (const FMATRIX *a, const DOUBLE s, FMATRIX *ad) |
| 行列とスカラーの引き算 | |
| INT FVALGAPI | fnFIE_mat_sub_vs (const FVECTOR *v, const DOUBLE s, FVECTOR *vd) |
| ベクトルとスカラーの引き算 | |
| INT FVALGAPI | fnFIE_vect_inner (const FVECTOR *v1, const FVECTOR *v2, DOUBLE *sd) |
| ベクトル内積計算 | |
| INT FVALGAPI | fnFIE_vect_cross (const FVECTOR *v1, const FVECTOR *v2, FVECTOR *vd) |
| ベクトル外積計算 | |
| INT FVALGAPI | fnFIE_vect_normalize (const FVECTOR *v, FVECTOR *vd) |
| 単位ベクトルの計算 | |
| DOUBLE FVALGAPI | fnFIE_vect_norm_l1 (const FVECTOR *v) |
| L1ノルムの算出 | |
| DOUBLE FVALGAPI | fnFIE_vect_norm_l2 (const FVECTOR *v) |
| L2ノルムの算出 | |
| DOUBLE FVALGAPI | fnFIE_vect_norm_l3 (const FVECTOR *v) |
| L3ノルムの算出 | |
| INT FVALGAPI | fnFIE_mat_det (const FMATRIX *a, DOUBLE *det) |
![[[OSS]]](oss.png) 行列式の計算 行列式の計算 | |
| INT FVALGAPI | fnFIE_mat_norm (const FMATRIX *a, INT type, DOUBLE *norm) |
![[[OSS]]](oss.png) 行列のノルムの計算 行列のノルムの計算 | |
| INT FVALGAPI | fnFIE_mat_rank (const FMATRIX *a, DOUBLE tol, INT *rank) |
![[[OSS]]](oss.png) 行列のランクの計算 行列のランクの計算 | |
| INT FVALGAPI | fnFIE_mat_svd (const FMATRIX *a, DOUBLE *sigma, FMATRIX *u, FMATRIX *vt) |
![[[OSS]]](oss.png) 行列の特異値分解 行列の特異値分解 | |
| INT FVALGAPI | fnFIE_mat_svd2 (const FMATRIX *a, FMATRIX **u, FVECTOR **sigma, FMATRIX **vt, INT mode, DOUBLE rcond, INT *rank) |
![[[OSS]]](oss.png) 行列の特異値分解 (convenience function) 行列の特異値分解 (convenience function) | |
| INT FVALGAPI | fnFIE_mat_chol (FMATRIX *a, CHAR *uplo) |
![[[OSS]]](oss.png) 行列のコレスキー分解 行列のコレスキー分解 | |
| INT FVALGAPI | fnFIE_mat_lu (FMATRIX *a, INT *pivot) |
![[[OSS]]](oss.png) 行列のLU分解 行列のLU分解 | |
| INT FVALGAPI | fnFIE_mat_qr (const FMATRIX *a, FMATRIX *q, FMATRIX *r) |
![[[OSS]]](oss.png) 行列のQR分解 行列のQR分解 | |
| INT FVALGAPI | fnFIE_mat_eig (const FMATRIX *a, FCOMPLEX *lambda, FCOMPLEX *vr, FCOMPLEX *vl) |
![[[OSS]]](oss.png) 行列の固有値・固有ベクトル計算 行列の固有値・固有ベクトル計算 | |
| INT FVALGAPI | fnFIE_mat_cond (const FMATRIX *a, INT type, DOUBLE *cond) |
![[[OSS]]](oss.png) 行列の条件数計算 行列の条件数計算 | |
| INT FVALGAPI | fnFIE_mat_rcond (const FMATRIX *a, DOUBLE *rcond) |
![[[OSS]]](oss.png) 行列の条件数の逆数計算 行列の条件数の逆数計算 | |
| INT FVALGAPI | fnFIE_mat_inverse3 (const FMATRIX *a, FMATRIX *ai, DOUBLE *det) |
![[[OSS]]](oss.png) 行列の逆行列計算(LAPACK使用) 行列の逆行列計算(LAPACK使用) | |
| INT FVALGAPI | fnFIE_mat_pseudo_inverse (const FMATRIX *a, FMATRIX *ai, DOUBLE threshold, INT *rank) |
![[[OSS]]](oss.png) 行列の擬似逆行列計算(LAPACK使用) 行列の擬似逆行列計算(LAPACK使用) | |
| INT FVALGAPI | fnFIE_mat_linsolve (const FMATRIX *a, FVECTOR *x, const FVECTOR *b, INT method, DOUBLE *residual, DOUBLE rcond, INT *rank) |
![[[OSS]]](oss.png) 連立一次方程式の計算 連立一次方程式の計算 | |
| INT FVALGAPI | fnFIE_mat_linsolve2 (const FMATRIX *a, FMATRIX *x, const FMATRIX *b, INT method, DOUBLE *residuals, DOUBLE rcond, INT *rank) |
![[[OSS]]](oss.png) 連立一次方程式の計算 連立一次方程式の計算 | |
関数
| INT FVALGAPI fnFIE_mat_inverse | ( | FMATRIX * | a | ) |
逆行列の算出
Gauss-Jordan法により、逆行列を求めます。 求められた逆行列は、元の行列 a に上書きされるので、 元の行列が必要な場合は、あらかじめコピーを取っておいてください。 また、入力する行列は正方行列でなければいけません。 入力された行列が正方行列でなかった場合には、F_ERR_INVALID_PARAM を返します。
- 引数:
-
[in,out] a 逆行列を計算する正方行列。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_CALC_IMPOSSIBLE 計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; DOUBLE det; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 b = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; printf( "a =\n" ); mat_print( a ); // a を上書きして a^-1 を計算 fnFIE_mat_inverse( a ); printf( "fnFIE_mat_inverse()\n" ); printf( "a^-1 = \n" ); mat_print( a ); // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; // a^-1 => b を計算 // inverse2 は a の内容を破壊するので注意 fnFIE_mat_inverse2( a, b, &det ); printf( "fnFIE_mat_inverse2()\n" ); printf( "det(a) = %f\n", det ); printf( "a^-1 = \n" ); mat_print( b ); a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; // a^-1 => b を計算 fnFIE_mat_inverse3( a, b, &det ); printf( "fnFIE_mat_inverse3()\n" ); printf( "det(a) = %f\n", det ); printf( "a^-1 = \n" ); mat_print( b ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] fnFIE_mat_inverse() a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] fnFIE_mat_inverse2() det(a) = 87.000000 a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] fnFIE_mat_inverse3() det(a) = 87.000000 a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] */
連立一次方程式の計算
Ax=b をLU分解を使用して解きます。
本関数では、係数行列 a の値は破壊されるため、 必要な場合は、あらかじめコピーを取っておいてください。
a, b, x の次元が不正な場合は F_ERR_INVALID_PARAM を返します。 また b と x の次元が同じでも、同じポインタを渡すことは出来ません。 正しい結果を得られません。
- 引数:
-
[in,out] a 係数行列A。AはNxN、つまり正方行列でなければいけません。 [in] b 連立一次方程式の右辺
b の次元はNでなければいけません。[out] x 答え
x の次元はNでなければいけません。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NOMEMORY メモリ不足エラー F_ERR_CALC_IMPOSSIBLE 計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FMATRIX *a=NULL; FVECTOR *v1=NULL, *v2=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; printf( "a =\n" ); mat_print( a ); printf( "v1 =\n" ); vect_print( v1 ); // a * v2 = v1 をv2について解く // a は破壊されるので注意 fnFIE_mat_solve( a, v1, v2 ); printf( "v2 = \n" ); vect_print( v2 ); // a * v2 = v1 となるか a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; fnFIE_mat_mul_av( a, v2, v1 ); printf( "a*v2 = \n" ); vect_print( v1 ); fnFIE_mat_afree( a ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +1.965517e+000 +7.356322e-001 -3.908046e-001 ] a*v2 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] */
逆行列の算出(LU分解採用)
LU分解を利用して、逆行列を求めます。
本関数では、入力の a の値は破壊されるため、 必要な場合は、あらかじめコピーを取っておいてください。
a_inv のサイズが a と違っていた場合は、エラーになります。
a_inv と a のサイズが同じでも、同じポインタを渡すことは出来ません。 正しい結果を得られません。
アルゴリズムは「C言語による最新アルゴリズム辞典」(ISBN4-87408-414-1)より。
- 引数:
-
[in,out] a 逆行列を計算する行列 [out] a_inv 求められた逆行列 [out] det aの行列式( det(a) )。 不要な場合はNULLを指定可能
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NOMEMORY メモリ不足エラー F_ERR_CALC_IMPOSSIBLE 計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; DOUBLE det; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 b = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; printf( "a =\n" ); mat_print( a ); // a を上書きして a^-1 を計算 fnFIE_mat_inverse( a ); printf( "fnFIE_mat_inverse()\n" ); printf( "a^-1 = \n" ); mat_print( a ); // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; // a^-1 => b を計算 // inverse2 は a の内容を破壊するので注意 fnFIE_mat_inverse2( a, b, &det ); printf( "fnFIE_mat_inverse2()\n" ); printf( "det(a) = %f\n", det ); printf( "a^-1 = \n" ); mat_print( b ); a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; // a^-1 => b を計算 fnFIE_mat_inverse3( a, b, &det ); printf( "fnFIE_mat_inverse3()\n" ); printf( "det(a) = %f\n", det ); printf( "a^-1 = \n" ); mat_print( b ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] fnFIE_mat_inverse() a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] fnFIE_mat_inverse2() det(a) = 87.000000 a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] fnFIE_mat_inverse3() det(a) = 87.000000 a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] */
行列の転置
a の転置行列を ad に出力します。
a の列数と ad の行数、 a の行数と ad の列数が それぞれ同じでなければいけません。
a が正方行列の場合に限り a と ad に同じポインタを渡すことが出来ます。 この場合、インプレース処理により転置が行われます。 そうでない場合は a と ad に同じポインタを渡すことは出来ません。
- 引数:
-
[in] a 入力行列 [out] ad 出力行列
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 b = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 5.0; a->m[0][2] = 9.0; a->m[0][3] =13.0; a->m[1][0] = 2.0; a->m[1][1] = 6.0; a->m[1][2] =10.0; a->m[1][3] =14.0; a->m[2][0] = 3.0; a->m[2][1] = 7.0; a->m[2][2] =11.0; a->m[2][3] =15.0; a->m[3][0] = 4.0; a->m[3][1] = 8.0; a->m[3][2] =12.0; a->m[3][3] =16.0; printf( "a =\n" ); mat_print( a ); // outplace fnFIE_mat_trans( a, b ); printf( "a^t =\n" ); mat_print( b ); // inplace - 正方行列の場合に限って可能です fnFIE_mat_trans( a, a ); printf( "a^t =\n" ); mat_print( a ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +5.000000e+000 +9.000000e+000 +1.300000e+001 ] [ +2.000000e+000 +6.000000e+000 +1.000000e+001 +1.400000e+001 ] [ +3.000000e+000 +7.000000e+000 +1.100000e+001 +1.500000e+001 ] [ +4.000000e+000 +8.000000e+000 +1.200000e+001 +1.600000e+001 ] a^t = [ +1.000000e+000 +2.000000e+000 +3.000000e+000 +4.000000e+000 ] [ +5.000000e+000 +6.000000e+000 +7.000000e+000 +8.000000e+000 ] [ +9.000000e+000 +1.000000e+001 +1.100000e+001 +1.200000e+001 ] [ +1.300000e+001 +1.400000e+001 +1.500000e+001 +1.600000e+001 ] a^t = [ +1.000000e+000 +2.000000e+000 +3.000000e+000 +4.000000e+000 ] [ +5.000000e+000 +6.000000e+000 +7.000000e+000 +8.000000e+000 ] [ +9.000000e+000 +1.000000e+001 +1.100000e+001 +1.200000e+001 ] [ +1.300000e+001 +1.400000e+001 +1.500000e+001 +1.600000e+001 ] */
| INT FVALGAPI fnFIE_mat_trace | ( | const FMATRIX * | a, | |
| DOUBLE * | trace | |||
| ) |
行列のトレースを計算
a のトレース(対角成分の和)を計算します。 a は正方行列である必要があります。
trace = sum( diag(a) )
- 引数:
-
[in] a 入力行列 [out] trace トレース
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 5.0; a->m[0][2] = 9.0; a->m[0][3] =13.0; a->m[1][0] = 2.0; a->m[1][1] = 6.0; a->m[1][2] =10.0; a->m[1][3] =14.0; a->m[2][0] = 3.0; a->m[2][1] = 7.0; a->m[2][2] =11.0; a->m[2][3] =15.0; a->m[3][0] = 4.0; a->m[3][1] = 8.0; a->m[3][2] =12.0; a->m[3][3] =16.0; printf( "a =\n" ); mat_print( a ); fnFIE_mat_trace( a, &d ); printf( "trace(a) =\n" ); printf( " %+0.6e\n\n", d ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +5.000000e+000 +9.000000e+000 +1.300000e+001 ] [ +2.000000e+000 +6.000000e+000 +1.000000e+001 +1.400000e+001 ] [ +3.000000e+000 +7.000000e+000 +1.100000e+001 +1.500000e+001 ] [ +4.000000e+000 +8.000000e+000 +1.200000e+001 +1.600000e+001 ] trace(a) = +3.400000e+001 */
行列とベクトルのかけ算
a * vs を計算します。
ベクトル/行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
vs と vd の次元が同じでも、同じポインタを渡すことは出来ません。 正しい結果を得られません。
- 引数:
-
[in] a 掛け合わせる行列(左) [in] vs 掛け合わせる列ベクトル(右) [out] vd 計算結果
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FMATRIX *a=NULL; FVECTOR *v1=NULL, *v2=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 4 ); // 3x4行列 a を確保 v1 = fnFIE_mat_valloc( 4 ); // 次元4のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[0][3] = 2.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[1][3] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; a->m[2][3] = 8.0; v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v1->v[3] = 2.0; printf( "a =\n" ); mat_print( a ); printf( "v1 =\n" ); vect_print( v1 ); // a * v1 => v2 を計算 fnFIE_mat_mul_av( a, v1, v2 ); printf( "a*v1 = v2 =\n" ); vect_print( v2 ); fnFIE_mat_afree( a ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 +2.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 +8.000000e+000 ] v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 +2.000000e+000 ] a*v1 = v2 = [ +4.900000e+001 +1.000000e+001 +4.400000e+001 ] */
ベクトルと行列のかけ算
vs * a を計算します。
ベクトル/行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
vs と vd の次元が同じでも、同じポインタを渡すことは出来ません。 正しい結果を得られません。
- 引数:
-
[in] vs 掛け合わせる行ベクトル(左) [in] a 掛け合わせる行列(右) [out] vd 計算結果(行ベクトル)
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FMATRIX *a=NULL; FVECTOR *v1=NULL, *v2=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 4 ); // 3x4行列 a を確保 v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 4 ); // 次元4のベクトル v2 を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[0][3] = 2.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[1][3] = 3.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; a->m[2][3] = 1.0; v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "a =\n" ); mat_print( a ); // a * v1 => v2 を計算 fnFIE_mat_mul_va( v1, a, v2 ); printf( "v1*a = v2 =\n" ); vect_print( v2 ); fnFIE_mat_afree( a ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 +2.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 +3.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 +1.000000e+000 ] v1*a = v2 = [ +4.300000e+001 +3.700000e+001 +7.000000e+000 +3.200000e+001 ] */
行列と行列のかけ算
a1 * a2 を計算します。
行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
a1 、 a2 の両方と ad は同じポインタを渡すことは出来ません。 正しい結果を得られません。 a1 と a2 は同じポインタを渡すことが出来ます。
- 引数:
-
[in] a1 掛け合わせる行列(左) [in] a2 掛け合わせる行列(右) [out] ad 計算結果
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL, *c=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 2 ); // 4x2行列 a を確保 b = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 b を確保 c = fnFIE_mat_aalloc( 4, 3 ); // 4x3行列 c を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[3][0] = 3.0; a->m[3][1] = 1.0; b->m[0][0] = 3.0; b->m[0][1] = 8.0; b->m[0][2] = 1.0; b->m[1][0] = 0.0; b->m[1][1] =-2.0; b->m[1][2] = 5.0; printf( "a =\n" ); mat_print( a ); printf( "b =\n" ); mat_print( b ); // a * b => c を計算 fnFIE_mat_mul_aa( a, b, c ); printf( "a*b = c =\n" ); mat_print( c ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); fnFIE_mat_afree( c ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 ] [ +2.000000e+000 +5.000000e+000 ] [ +3.000000e+000 +1.000000e+000 ] b = [ +3.000000e+000 +8.000000e+000 +1.000000e+000 ] [ +0.000000e+000 -2.000000e+000 +5.000000e+000 ] a*b = c = [ +3.000000e+000 +2.000000e+000 +1.600000e+001 ] [ +1.200000e+001 +3.600000e+001 -6.000000e+000 ] [ +6.000000e+000 +6.000000e+000 +2.700000e+001 ] [ +9.000000e+000 +2.200000e+001 +8.000000e+000 ] */
行列とスカラーのかけ算
行列 a の各要素に、スカラ量 s をかけ算します
行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
a と ad は同じポインタを渡すことが出来ます。
- 引数:
-
[in] a 掛けられる行列 [in] s 掛ける値 [out] ad 計算結果
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 b = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; printf( "a =\n" ); mat_print( a ); // a * b => c を計算 fnFIE_mat_mul_as( a, 8.0, b ); printf( "a*8 = b =\n" ); mat_print( b ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] a*8 = b = [ +8.000000e+000 +2.400000e+001 +2.400000e+001 ] [ +3.200000e+001 -1.600000e+001 +8.000000e+000 ] [ +1.600000e+001 +4.000000e+001 -8.000000e+000 ] */
ベクトルとスカラーのかけ算
ベクトル v の各要素に、スカラ量 s をかけ算します
ベクトルの次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
v と vd は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v 掛けられるベクトル [in] s 掛ける値 [out] vd 結果ベクトル
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; printf( "v1 =\n" ); vect_print( v1 ); // v1 * 8.0 => v2 を計算 fnFIE_mat_mul_vs( v1, 8.0, v2 ); printf( "v1*8 = v2 =\n" ); vect_print( v2 ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v1*8 = v2 = [ +2.400000e+001 +4.800000e+001 +6.400000e+001 ] */
行列の足し算
a1 + a2 を計算します。
行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
a1 と a2 と ad は同じポインタを渡すことが出来ます。
- 引数:
-
[in] a1 足される行列 [in] a2 足す行列 [out] ad 結果行列
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL, *c=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 a を確保 b = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 b を確保 c = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 c を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; b->m[0][0] = 3.0; b->m[0][1] = 8.0; b->m[0][2] = 1.0; b->m[1][0] = 0.0; b->m[1][1] =-2.0; b->m[1][2] = 5.0; printf( "a =\n" ); mat_print( a ); printf( "b =\n" ); mat_print( b ); // a + b => c を計算 fnFIE_mat_sum_aa( a, b, c ); printf( "a+b = c =\n" ); mat_print( c ); // a - b => c を計算 fnFIE_mat_sub_aa( a, b, c ); printf( "a-b = c =\n" ); mat_print( c ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); fnFIE_mat_afree( c ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] b = [ +3.000000e+000 +8.000000e+000 +1.000000e+000 ] [ +0.000000e+000 -2.000000e+000 +5.000000e+000 ] a+b = c = [ +4.000000e+000 +1.100000e+001 +4.000000e+000 ] [ +4.000000e+000 -4.000000e+000 +6.000000e+000 ] a-b = c = [ -2.000000e+000 -5.000000e+000 +2.000000e+000 ] [ +4.000000e+000 +0.000000e+000 -4.000000e+000 ] */
ベクトルの足し算
v1 + v2 を計算します。
ベクトルの次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
v1 と v2 と vd は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v1 足されるベクトル [in] v2 足すベクトル [out] vd 結果行列
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 + v2 => vd を計算 fnFIE_mat_sum_vv( v1, v2, vd ); printf( "v1+v2 = vd =\n" ); vect_print( vd ); // v1 - v2 => vd を計算 fnFIE_mat_sub_vv( v1, v2, vd ); printf( "v1-v2 = vd =\n" ); vect_print( vd ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1+v2 = vd = [ +7.000000e+000 +1.400000e+001 +2.300000e+001 ] v1-v2 = vd = [ -1.000000e+000 -2.000000e+000 -7.000000e+000 ] */
行列とスカラーの足し算
行列 a の各要素に s を足し算します。
行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
a と ad は同じポインタを渡すことが出来ます。
- 引数:
-
[in] a 足される行列 [in] s 足す値 [out] ad 結果行列
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 b = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; printf( "a =\n" ); mat_print( a ); // a + 8.0 => b を計算 fnFIE_mat_sum_as( a, 8.0, b ); printf( "a+8.0 = b =\n" ); mat_print( b ); // a - 8.0 => b を計算 fnFIE_mat_sub_as( a, 8.0, b ); printf( "a-8.0 = b =\n" ); mat_print( b ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] a+8.0 = b = [ +9.000000e+000 +1.100000e+001 +1.100000e+001 ] [ +1.200000e+001 +6.000000e+000 +9.000000e+000 ] [ +1.000000e+001 +1.300000e+001 +7.000000e+000 ] a-8.0 = b = [ -7.000000e+000 -5.000000e+000 -5.000000e+000 ] [ -4.000000e+000 -1.000000e+001 -7.000000e+000 ] [ -6.000000e+000 -3.000000e+000 -9.000000e+000 ] */
ベクトルとスカラーの足し算
ベクトル v の各要素に、スカラ量 s を足し算します。
ベクトルの次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
v と vd は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v 足されるベクトル [in] s 足す値 [out] vd 結果ベクトル
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; printf( "v1 =\n" ); vect_print( v1 ); // v1 + 8.0 => v2 を計算 fnFIE_mat_sum_vs( v1, 8.0, v2 ); printf( "v1+8.0 = v2 =\n" ); vect_print( v2 ); // v1 - 8.0 => v2 を計算 fnFIE_mat_sub_vs( v1, 8.0, v2 ); printf( "v1-8.0 = v2 =\n" ); vect_print( v2 ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v1+8.0 = v2 = [ +1.100000e+001 +1.400000e+001 +1.600000e+001 ] v1-8.0 = v2 = [ -5.000000e+000 -2.000000e+000 +0.000000e+000 ] */
行列の引き算
a1 - a2 を計算します。
行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
a1 と a2 と ad は同じポインタを渡すことが出来ます。
- 引数:
-
[in] a1 引かれる行列 [in] a2 引く行列 [out] ad 結果行列
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL, *c=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 a を確保 b = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 b を確保 c = fnFIE_mat_aalloc( 2, 3 ); // 2x3行列 c を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; b->m[0][0] = 3.0; b->m[0][1] = 8.0; b->m[0][2] = 1.0; b->m[1][0] = 0.0; b->m[1][1] =-2.0; b->m[1][2] = 5.0; printf( "a =\n" ); mat_print( a ); printf( "b =\n" ); mat_print( b ); // a + b => c を計算 fnFIE_mat_sum_aa( a, b, c ); printf( "a+b = c =\n" ); mat_print( c ); // a - b => c を計算 fnFIE_mat_sub_aa( a, b, c ); printf( "a-b = c =\n" ); mat_print( c ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); fnFIE_mat_afree( c ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] b = [ +3.000000e+000 +8.000000e+000 +1.000000e+000 ] [ +0.000000e+000 -2.000000e+000 +5.000000e+000 ] a+b = c = [ +4.000000e+000 +1.100000e+001 +4.000000e+000 ] [ +4.000000e+000 -4.000000e+000 +6.000000e+000 ] a-b = c = [ -2.000000e+000 -5.000000e+000 +2.000000e+000 ] [ +4.000000e+000 +0.000000e+000 -4.000000e+000 ] */
ベクトルの引き算
v1 - v2 を計算します。
ベクトルの次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
v1 と v2 と vd は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v1 引かれるベクトル [in] v2 引くベクトル [out] vd 結果ベクトル
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 + v2 => vd を計算 fnFIE_mat_sum_vv( v1, v2, vd ); printf( "v1+v2 = vd =\n" ); vect_print( vd ); // v1 - v2 => vd を計算 fnFIE_mat_sub_vv( v1, v2, vd ); printf( "v1-v2 = vd =\n" ); vect_print( vd ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1+v2 = vd = [ +7.000000e+000 +1.400000e+001 +2.300000e+001 ] v1-v2 = vd = [ -1.000000e+000 -2.000000e+000 -7.000000e+000 ] */
行列とスカラーの引き算
行列 a の各要素から、スカラ量 s を引き算します。
行列の次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
a と ad は同じポインタを渡すことが出来ます。
- 引数:
-
[in] a 引かれる行列 [in] s 引く値 [out] ad 結果行列
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 b = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; printf( "a =\n" ); mat_print( a ); // a + 8.0 => b を計算 fnFIE_mat_sum_as( a, 8.0, b ); printf( "a+8.0 = b =\n" ); mat_print( b ); // a - 8.0 => b を計算 fnFIE_mat_sub_as( a, 8.0, b ); printf( "a-8.0 = b =\n" ); mat_print( b ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] a+8.0 = b = [ +9.000000e+000 +1.100000e+001 +1.100000e+001 ] [ +1.200000e+001 +6.000000e+000 +9.000000e+000 ] [ +1.000000e+001 +1.300000e+001 +7.000000e+000 ] a-8.0 = b = [ -7.000000e+000 -5.000000e+000 -5.000000e+000 ] [ -4.000000e+000 -1.000000e+001 -7.000000e+000 ] [ -6.000000e+000 -3.000000e+000 -9.000000e+000 ] */
ベクトルとスカラーの引き算
ベクトル v の各要素から、スカラ量 s を引き算します。
ベクトルの次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
v と vd は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v 引かれるベクトル [in] s 引く値 [out] vd 結果ベクトル
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; printf( "v1 =\n" ); vect_print( v1 ); // v1 + 8.0 => v2 を計算 fnFIE_mat_sum_vs( v1, 8.0, v2 ); printf( "v1+8.0 = v2 =\n" ); vect_print( v2 ); // v1 - 8.0 => v2 を計算 fnFIE_mat_sub_vs( v1, 8.0, v2 ); printf( "v1-8.0 = v2 =\n" ); vect_print( v2 ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v1+8.0 = v2 = [ +1.100000e+001 +1.400000e+001 +1.600000e+001 ] v1-8.0 = v2 = [ -5.000000e+000 -2.000000e+000 +0.000000e+000 ] */
ベクトル内積計算
v1v2 の値を計算します。
ベクトル V1 と V2 との内積は次式で定義されます。
![\[ {\bf V1} \cdot {\bf V2} \equiv \sum_{i=0}^{dim} V1_i V2_i \]](form_637.png)
ここで、dim は各ベクトルの次元を表します。
ベクトルの次元が正しくない場合は F_ERR_INVALID_PARAM エラーを返します。
v1 と v2 は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v1 内積を計算するベクトル [in] v2 内積を計算するベクトル [out] sd 計算結果
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 dot v2 => d を計算 fnFIE_vect_inner( v1, v2, &d ); printf( "v1 dot v2 = d =\n" ); printf( " %f\n\n", d ); // v1 x v2 => vd を計算 fnFIE_vect_cross( v1, v2, vd ); printf( "v1 x v2 = vd =\n" ); vect_print( vd ); // normalize(v1) => vd を計算 fnFIE_vect_normalize( v1, vd ); printf( "normalize(v1) = vd =\n" ); vect_print( vd ); // L1-norm(v1) => d を計算 d = fnFIE_vect_norm_l1( v1 ); printf( "L1-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // L2-norm(v1) => d を計算 d = fnFIE_vect_norm_l2( v1 ); printf( "L2-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // INF-norm(v1) => d を計算 d = fnFIE_vect_norm_l3( v1 ); printf( "INF-norm(v1) = d =\n" ); printf( " %f\n\n", d ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1 dot v2 = d = 180.000000 v1 x v2 = vd = [ +2.600000e+001 -1.300000e+001 +0.000000e+000 ] normalize(v1) = vd = [ +2.873479e-001 +5.746958e-001 +7.662610e-001 ] L1-norm(v1) = d = 17.000000 L2-norm(v1) = d = 10.440307 INF-norm(v1) = d = 8.000000 */
ベクトル外積計算
v1 x v2 の値を計算します。 v1, v2, vd の次元はすべて3でなければいけません。
ベクトル v1 と v2 の外積は次式で定義されます。
![\[ {\bf V1} \times {\bf V2} \equiv \left( V1_1 V2_2 - V1_2 V2_1, V1_2 V2_0 - V1_0 V2_2, V1_0 V2_1 - V1_1 V2_0 \right) \]](form_638.png)
v1 、 v2 の両方と vd は同じポインタを渡すことは出来ません。 正しい結果を得られません。 v1 と v2 は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v1 外積を計算するベクトル [in] v2 外積を計算するベクトル [out] vd 計算結果ベクトル
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 dot v2 => d を計算 fnFIE_vect_inner( v1, v2, &d ); printf( "v1 dot v2 = d =\n" ); printf( " %f\n\n", d ); // v1 x v2 => vd を計算 fnFIE_vect_cross( v1, v2, vd ); printf( "v1 x v2 = vd =\n" ); vect_print( vd ); // normalize(v1) => vd を計算 fnFIE_vect_normalize( v1, vd ); printf( "normalize(v1) = vd =\n" ); vect_print( vd ); // L1-norm(v1) => d を計算 d = fnFIE_vect_norm_l1( v1 ); printf( "L1-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // L2-norm(v1) => d を計算 d = fnFIE_vect_norm_l2( v1 ); printf( "L2-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // INF-norm(v1) => d を計算 d = fnFIE_vect_norm_l3( v1 ); printf( "INF-norm(v1) = d =\n" ); printf( " %f\n\n", d ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1 dot v2 = d = 180.000000 v1 x v2 = vd = [ +2.600000e+001 -1.300000e+001 +0.000000e+000 ] normalize(v1) = vd = [ +2.873479e-001 +5.746958e-001 +7.662610e-001 ] L1-norm(v1) = d = 17.000000 L2-norm(v1) = d = 10.440307 INF-norm(v1) = d = 8.000000 */
単位ベクトルの計算
ベクトル v の単位ベクトルを計算します。
vd の L2ノルム が 1.0 となるように、 スカラ係数を v に掛け合わせ、 vd に出力します。
v と vd は同じポインタを渡すことが出来ます。
- 引数:
-
[in] v 単位ベクトル化するベクトル [out] vd 結果ベクトル
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 dot v2 => d を計算 fnFIE_vect_inner( v1, v2, &d ); printf( "v1 dot v2 = d =\n" ); printf( " %f\n\n", d ); // v1 x v2 => vd を計算 fnFIE_vect_cross( v1, v2, vd ); printf( "v1 x v2 = vd =\n" ); vect_print( vd ); // normalize(v1) => vd を計算 fnFIE_vect_normalize( v1, vd ); printf( "normalize(v1) = vd =\n" ); vect_print( vd ); // L1-norm(v1) => d を計算 d = fnFIE_vect_norm_l1( v1 ); printf( "L1-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // L2-norm(v1) => d を計算 d = fnFIE_vect_norm_l2( v1 ); printf( "L2-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // INF-norm(v1) => d を計算 d = fnFIE_vect_norm_l3( v1 ); printf( "INF-norm(v1) = d =\n" ); printf( " %f\n\n", d ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1 dot v2 = d = 180.000000 v1 x v2 = vd = [ +2.600000e+001 -1.300000e+001 +0.000000e+000 ] normalize(v1) = vd = [ +2.873479e-001 +5.746958e-001 +7.662610e-001 ] L1-norm(v1) = d = 17.000000 L2-norm(v1) = d = 10.440307 INF-norm(v1) = d = 8.000000 */
| DOUBLE FVALGAPI fnFIE_vect_norm_l1 | ( | const FVECTOR * | v | ) |
L1ノルムの算出
ベクトル v のL1ノルムを計算します。 L1ノルムは下記式にて定義されます。
![\[ {\bf V} = (v_0, v_1, \ldots , v_n) \]](form_639.png)
![\[ \|{\bf V}\|_1 = \sum_{i=1}^{n}{|x_i|} \]](form_640.png)
- 引数:
-
[in] v L1ノルムを計算するベクトル
- 戻り値:
- L1ノルムの値。 不正なベクトルが与えられた場合 ライセンスエラー、または未初期化エラーが発生した場合には、0.0を返します。
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 dot v2 => d を計算 fnFIE_vect_inner( v1, v2, &d ); printf( "v1 dot v2 = d =\n" ); printf( " %f\n\n", d ); // v1 x v2 => vd を計算 fnFIE_vect_cross( v1, v2, vd ); printf( "v1 x v2 = vd =\n" ); vect_print( vd ); // normalize(v1) => vd を計算 fnFIE_vect_normalize( v1, vd ); printf( "normalize(v1) = vd =\n" ); vect_print( vd ); // L1-norm(v1) => d を計算 d = fnFIE_vect_norm_l1( v1 ); printf( "L1-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // L2-norm(v1) => d を計算 d = fnFIE_vect_norm_l2( v1 ); printf( "L2-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // INF-norm(v1) => d を計算 d = fnFIE_vect_norm_l3( v1 ); printf( "INF-norm(v1) = d =\n" ); printf( " %f\n\n", d ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1 dot v2 = d = 180.000000 v1 x v2 = vd = [ +2.600000e+001 -1.300000e+001 +0.000000e+000 ] normalize(v1) = vd = [ +2.873479e-001 +5.746958e-001 +7.662610e-001 ] L1-norm(v1) = d = 17.000000 L2-norm(v1) = d = 10.440307 INF-norm(v1) = d = 8.000000 */
| DOUBLE FVALGAPI fnFIE_vect_norm_l2 | ( | const FVECTOR * | v | ) |
L2ノルムの算出
ベクトル v のL2ノルムを計算します。 L2ノルムは下記式にて定義されます。
![\[ \mbox{\boldmath$V$} = (v_0, v_1, \ldots , v_n) \]](form_641.png)
![\[ \|\mbox{\boldmath$V$}\|_2 = \sqrt{|v_0|^2 + |v_1|^2 + \cdots + |v_n|^2 } \]](form_642.png)
- 引数:
-
[in] v L2ノルムを計算するベクトル
- 戻り値:
- L2ノルムの値 不正なベクトルが与えられた場合、 ライセンスエラー、または未初期化エラーが発生した場合には、0.0を返します。
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 dot v2 => d を計算 fnFIE_vect_inner( v1, v2, &d ); printf( "v1 dot v2 = d =\n" ); printf( " %f\n\n", d ); // v1 x v2 => vd を計算 fnFIE_vect_cross( v1, v2, vd ); printf( "v1 x v2 = vd =\n" ); vect_print( vd ); // normalize(v1) => vd を計算 fnFIE_vect_normalize( v1, vd ); printf( "normalize(v1) = vd =\n" ); vect_print( vd ); // L1-norm(v1) => d を計算 d = fnFIE_vect_norm_l1( v1 ); printf( "L1-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // L2-norm(v1) => d を計算 d = fnFIE_vect_norm_l2( v1 ); printf( "L2-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // INF-norm(v1) => d を計算 d = fnFIE_vect_norm_l3( v1 ); printf( "INF-norm(v1) = d =\n" ); printf( " %f\n\n", d ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1 dot v2 = d = 180.000000 v1 x v2 = vd = [ +2.600000e+001 -1.300000e+001 +0.000000e+000 ] normalize(v1) = vd = [ +2.873479e-001 +5.746958e-001 +7.662610e-001 ] L1-norm(v1) = d = 17.000000 L2-norm(v1) = d = 10.440307 INF-norm(v1) = d = 8.000000 */
| DOUBLE FVALGAPI fnFIE_vect_norm_l3 | ( | const FVECTOR * | v | ) |
L3ノルムの算出
ベクトル v のL3ノルムを計算します。 L3ノルムは下記式にて定義されます。
![\[ {\bf V} = (v_0, v_1, \ldots , v_n) \]](form_639.png)
![\[ \|{\bf V}\|_3 = \max( |v_0|, |v_1|, \ldots , |v_n| ) \]](form_643.png)
- 引数:
-
[in] v L3ノルムを計算するベクトル
- 戻り値:
- L3ノルムの値 不正なベクトルが与えられた場合、 ライセンスエラー、または未初期化エラーが発生した場合には、0.0を返します。
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FVECTOR *v1=NULL, *v2=NULL, *vd=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); v1 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v1 を確保 v2 = fnFIE_mat_valloc( 3 ); // 次元3のベクトル v2 を確保 vd = fnFIE_mat_valloc( 3 ); // 次元3のベクトル vd を確保 // 入力値をセット v1->v[0] = 3.0; v1->v[1] = 6.0; v1->v[2] = 8.0; v2->v[0] = 4.0; v2->v[1] = 8.0; v2->v[2] = 15.0; printf( "v1 =\n" ); vect_print( v1 ); printf( "v2 =\n" ); vect_print( v2 ); // v1 dot v2 => d を計算 fnFIE_vect_inner( v1, v2, &d ); printf( "v1 dot v2 = d =\n" ); printf( " %f\n\n", d ); // v1 x v2 => vd を計算 fnFIE_vect_cross( v1, v2, vd ); printf( "v1 x v2 = vd =\n" ); vect_print( vd ); // normalize(v1) => vd を計算 fnFIE_vect_normalize( v1, vd ); printf( "normalize(v1) = vd =\n" ); vect_print( vd ); // L1-norm(v1) => d を計算 d = fnFIE_vect_norm_l1( v1 ); printf( "L1-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // L2-norm(v1) => d を計算 d = fnFIE_vect_norm_l2( v1 ); printf( "L2-norm(v1) = d =\n" ); printf( " %f\n\n", d ); // INF-norm(v1) => d を計算 d = fnFIE_vect_norm_l3( v1 ); printf( "INF-norm(v1) = d =\n" ); printf( " %f\n\n", d ); fnFIE_mat_vfree( v1 ); fnFIE_mat_vfree( v2 ); fnFIE_mat_vfree( vd ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 v1 = [ +3.000000e+000 +6.000000e+000 +8.000000e+000 ] v2 = [ +4.000000e+000 +8.000000e+000 +1.500000e+001 ] v1 dot v2 = d = 180.000000 v1 x v2 = vd = [ +2.600000e+001 -1.300000e+001 +0.000000e+000 ] normalize(v1) = vd = [ +2.873479e-001 +5.746958e-001 +7.662610e-001 ] L1-norm(v1) = d = 17.000000 L2-norm(v1) = d = 10.440307 INF-norm(v1) = d = 8.000000 */
| INT FVALGAPI fnFIE_mat_det | ( | const FMATRIX * | a, | |
| DOUBLE * | det | |||
| ) |
![[[OSS]]](oss.png) 行列式の計算
行列式の計算
NxN 行列 a の行列式 (det(a)) を計算します。 入力行列 a は正方行列で無ければいけません。
- 覚え書き:
- 本関数ではLU分解を用いた手法により行列式を求めます。 LU分解にはLAPACKの DGETRF を使用します。
[L,U] = lu(a) s = -1 or 1 ( compute from pivot info ) det = s*product( diag(U) )
- 引数:
-
[in] a 入力NxN行列 [out] det 行列式の値
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM 入力パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 入力値をセット fnFIE_mat_rand( a ); printf( "a =\n" ); mat_print( a ); fnFIE_mat_det( a, &d ); printf( "det(a) =\n" ); printf( " %+0.6e\n\n", d ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +2.509236e-001 +6.805727e-001 +4.609582e-002 +3.209734e-001 ] [ +6.768162e-001 +1.553593e-001 +4.346949e-002 +6.005672e-001 ] [ +1.164237e-001 +9.243582e-001 +6.038657e-001 +7.878644e-001 ] [ +1.909307e-001 +7.638308e-001 +6.685157e-001 +7.029740e-001 ] det(a) = +4.434235e-002 */
| INT FVALGAPI fnFIE_mat_norm | ( | const FMATRIX * | a, | |
| INT | type, | |||
| DOUBLE * | norm | |||
| ) |
![[[OSS]]](oss.png) 行列のノルムの計算
行列のノルムの計算
MxN行列 A のノルムを計算します。 1-norm, 2-norm, infinity norm, Frobenius norm の4種類のうち 何れかが計算できます。
- 覚え書き:
- 本関数では LAPACK の下記の関数を使用してノルムを計算します。
- 1-norm, infinity norm, frobenius norm の場合 : DLANGE
- 2-norm の場合 : DGESDD
- 引数:
-
[in] a 入力MxN行列 [in] type 求めるノルムの種類 - 1 : 1-norm
- 2 : 2-norm (特異値の最大値)
- I32_MAX : infinity norm
- -1 : Frobenius norm
[out] norm ノルムの値
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 入力値をセット fnFIE_mat_rand( a ); printf( "a =\n" ); mat_print( a ); // L1-norm fnFIE_mat_norm( a, 1, &d ); printf( "norm(a, 1) =\n" ); printf( " %+0.6e\n\n", d ); // L2-norm fnFIE_mat_norm( a, 2, &d ); printf( "norm(a, 2) =\n" ); printf( " %+0.6e\n\n", d ); // INF-norm fnFIE_mat_norm( a, INT_MAX, &d ); printf( "norm(a, inf) =\n" ); printf( " %+0.6e\n\n", d ); // frobenius-norm fnFIE_mat_norm( a, -1, &d ); printf( "norm(a, fro) =\n" ); printf( " %+0.6e\n\n", d ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +2.509236e-001 +6.805727e-001 +4.609582e-002 +3.209734e-001 ] [ +6.768162e-001 +1.553593e-001 +4.346949e-002 +6.005672e-001 ] [ +1.164237e-001 +9.243582e-001 +6.038657e-001 +7.878644e-001 ] [ +1.909307e-001 +7.638308e-001 +6.685157e-001 +7.029740e-001 ] norm(a, 1) = +2.524121e+000 norm(a, 2) = +2.059209e+000 norm(a, inf) = +2.432512e+000 norm(a, fro) = +2.211432e+000 */
| INT FVALGAPI fnFIE_mat_rank | ( | const FMATRIX * | a, | |
| DOUBLE | tol, | |||
| INT * | rank | |||
| ) |
![[[OSS]]](oss.png) 行列のランクの計算
行列のランクの計算
入力行列 a のランクを計算します。
- 覚え書き:
- 本関数では LAPACK の DGESDD, DLAMCH を使用してランクを計算します。 ランクの計算には多数の方法が有りますが、 本関数では特異値分解を用いた手法を使用します。
- pseudo code
s = svd(a) if tol<0.0 { eps = dlamch('E') tol = max(a->row,a->col) * max(s) * eps } rank = sum( s>tol )
- 引数:
-
[in] a 入力MxN行列 [in] tol 0と見なす閾値
tol<0.0 の値が指定されたときは、max(a->row,a->col) * max(s) * eps の値を使用します。[out] rank ランクの値
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
#include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; INT r; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 4x4 full rank fnFIE_mat_rand( a ); printf( "a =\n" ); mat_print( a ); fnFIE_mat_rank( a, -1.0, &r ); printf( "rank(a) =\n" ); printf( " %d\n\n", r ); // 4x4 rank=3 fnFIE_mat_eye( a ); a->m[3][3] = 0.0; printf( "a =\n" ); mat_print( a ); fnFIE_mat_rank( a, -1.0, &r ); printf( "rank(a) =\n" ); printf( " %d\n\n", r ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +2.509236e-001 +6.805727e-001 +4.609582e-002 +3.209734e-001 ] [ +6.768162e-001 +1.553593e-001 +4.346949e-002 +6.005672e-001 ] [ +1.164237e-001 +9.243582e-001 +6.038657e-001 +7.878644e-001 ] [ +1.909307e-001 +7.638308e-001 +6.685157e-001 +7.029740e-001 ] rank(a) = 4 a = [ +1.000000e+000 +0.000000e+000 +0.000000e+000 +0.000000e+000 ] [ +0.000000e+000 +1.000000e+000 +0.000000e+000 +0.000000e+000 ] [ +0.000000e+000 +0.000000e+000 +1.000000e+000 +0.000000e+000 ] [ +0.000000e+000 +0.000000e+000 +0.000000e+000 +0.000000e+000 ] rank(a) = 3 */
![[[OSS]]](oss.png) 行列の特異値分解
行列の特異値分解
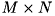 の入力行列 A の特異値分解を行います。
の入力行列 A の特異値分解を行います。 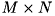 行列の特異値分解は
行列の特異値分解は
![\[ {\bf A} = {\bf U} \Sigma {\bf V}^T \]](form_1014.png)
で与えられます。ここで 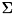 は
は 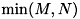 個の対角要素を 除いて全て 0 の
個の対角要素を 除いて全て 0 の 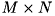 行列、
行列、 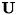 は
は 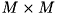 の直交行列、
の直交行列、 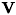 は
は 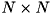 の直交行列です。
の直交行列です。  の実対角要素は
の実対角要素は 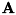 の特異値です。
の特異値です。 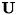 と
と 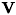 の最初の
の最初の 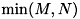 列は行列
列は行列 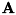 の左及び右特異ベクトルです。
の左及び右特異ベクトルです。
本関数は 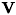 では無く
では無く 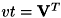 を返すことに注意して下さい。
を返すことに注意して下さい。
上記条件を満たした場合、u または vt と a は同じポインタを渡すことが出来ます。
- economy size matrix
- u に
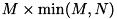 、 vt に
、 vt に 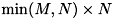 のサイズの行列を渡すと、 u には
のサイズの行列を渡すと、 u には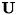 の最初
の最初 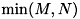 列(左特異ベクトル、列方向)が、 vt には
列(左特異ベクトル、列方向)が、 vt には 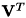 の最初の
の最初の 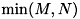 行(右特異ベクトル、行方向)が格納されます。
行(右特異ベクトル、行方向)が格納されます。
- 覚え書き:
- 本関数では LAPACK の DGESDD を使用して特異値分解を行います。
- 引数:
-
[in] a 入力 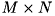 行列
行列 [out] sigma 大きい順( sigma(i) >= sigma(i+1) )にソートされた 特異値配列。 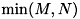 個の領域が必要。
個の領域が必要。 [out] u 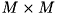 直交行列
直交行列 
計算不要な場合はNULLを指定して下さい。
u にNULLを指定する場合は vt もNULLを指定しなければいけません。[out] vt 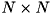 直交行列
直交行列 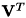
計算不要な場合はNULLを指定して下さい。
vt にNULLを指定する場合は u もNULLを指定しなければいけません。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" #include "oal_aloc.h" //メモリ管理 static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *u=NULL, *vt=NULL; INT i; DOUBLE *sigma; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 2 ); // 3x2行列 a を確保 u = fnFIE_mat_aalloc( 3, 3 ); // MxM (=3x3)行列 u を確保 vt = fnFIE_mat_aalloc( 2, 2 ); // NxN (=2x2)行列 vt を確保 sigma = (DOUBLE*)fnOAL_malloc( sizeof(DOUBLE)*2 ); // min(M,N) (=2)配列を確保 // 行列をセット fnFIE_mat_rand( a ); printf( "a =\n" ); mat_print( a ); // sigma だけを求める fnFIE_mat_svd( a, sigma, NULL, NULL ); printf( "sigma = \n" ); for( i=0; i<2; i++ ) printf( " %+0.6e\n", sigma[i] ); printf( "\n" ); // sigma, u, vt を求める fnFIE_mat_svd( a, sigma, u, vt ); printf( "sigma = \n" ); for( i=0; i<2; i++ ) printf( " %+0.6e\n", sigma[i] ); printf( "u =\n" ); mat_print( u ); printf( "vt =\n" ); mat_print( vt ); fnFIE_mat_afree( a ); fnFIE_mat_afree( u ); fnFIE_mat_afree( vt ); fnOAL_free( sigma ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +2.509236e-001 +6.805727e-001 ] [ +4.609582e-002 +3.209734e-001 ] [ +6.768162e-001 +1.553593e-001 ] sigma = +9.216314e-001 +5.139096e-001 sigma = +9.216314e-001 +5.139096e-001 u = [ -7.324410e-001 -5.165248e-001 -4.435452e-001 ] [ -2.932841e-001 -3.485590e-001 +8.902197e-001 ] [ -6.144222e-001 +7.821181e-001 +1.038104e-001 ] vt = [ -6.652951e-001 -7.465805e-001 ] [ +7.465805e-001 -6.652951e-001 ] */
| INT FVALGAPI fnFIE_mat_svd2 | ( | const FMATRIX * | a, | |
| FMATRIX ** | u, | |||
| FVECTOR ** | sigma, | |||
| FMATRIX ** | vt, | |||
| INT | mode, | |||
| DOUBLE | rcond, | |||
| INT * | rank | |||
| ) |
![[[OSS]]](oss.png) 行列の特異値分解 (convenience function)
行列の特異値分解 (convenience function)
 の入力行列 A の特異値分解を行います。 本関数は fnFIE_mat_svd() の利便性を高めたバージョンです。 fnFIE_mat_svd() との違いは u , sigma または vt の指定方法 にあります。fnFIE_mat_svd() ではこれらを事前にユーザーが確保しておかなければ ならないのに対して、本関数では関数内部で必用なサイズを自動的に確保します。 また u または vt のどちらか一方のみを取得出来ることも異なる点の一つです。 加えて、本関数ではランクの計算を同時に行うことが出来ます。
の入力行列 A の特異値分解を行います。 本関数は fnFIE_mat_svd() の利便性を高めたバージョンです。 fnFIE_mat_svd() との違いは u , sigma または vt の指定方法 にあります。fnFIE_mat_svd() ではこれらを事前にユーザーが確保しておかなければ ならないのに対して、本関数では関数内部で必用なサイズを自動的に確保します。 また u または vt のどちらか一方のみを取得出来ることも異なる点の一つです。 加えて、本関数ではランクの計算を同時に行うことが出来ます。
 行列の特異値分解は
行列の特異値分解は
![\[ {\bf A} = {\bf U} \Sigma {\bf V}^T \]](form_1014.png)
で与えられます。ここで  は
は 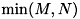 個の対角要素を 除いて全て 0 の
個の対角要素を 除いて全て 0 の 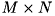 行列、
行列、 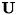 は
は 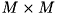 の直交行列、
の直交行列、 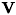 は
は 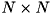 の直交行列です。
の直交行列です。 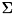 の実対角要素は
の実対角要素は 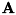 の特異値です。
の特異値です。 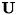 と
と 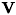 の最初の
の最初の 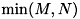 列は行列
列は行列 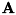 の左及び右特異ベクトルです。
の左及び右特異ベクトルです。
本関数は 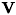 では無く
では無く 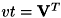 を返すことに注意して下さい。
を返すことに注意して下さい。
本関数では fnFIE_mat_svd() と異なり u または vt と a に 同じポインタを渡すことはできません。また u, vt, sigma に NULL以外を渡す場合には、 u, vt, には fnFIE_mat_aalloc() sigma には fnFIE_mat_valloc() で確保された行列・ベクトルを渡さなければなりません。
rank にNULL以外が渡された場合、本関数はランクの計算を共に行います。 ランクの計算は計算された特異値を使用して次のアルゴリズムで行われます。
pseudo code:
s = svd(a)
if rcond<0.0 rcond = dlamch('E')
tol = rcond * s[0]
rank = sum( s>tol )
- 覚え書き:
- 本関数は内部で fnFIE_mat_svd() を呼び出して演算を行います。
- 引数:
-
[in] a 入力 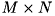 行列
行列 [out] u 直交行列 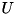 のポインタ
のポインタ
計算不要な場合はNULLを指定して下さい。
u != NULL の場合 *u は NULL 又は fnFIE_mat_aalloc() で確保されたFMATRIXのポインタでなければなりません。[out] sigma 大きい順( sigma(i) >= sigma(i+1) )にソートされた特異値配列。 計算不要な場合はNULLを指定して下さい。
sigma != NULL の場合 *sigma は NULL 又は fnFIE_mat_valloc() で確保されたFVECTORのポインタでなければなりません。[out] vt 直交行列 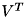
計算不要な場合はNULLを指定して下さい。
vt != NULL の場合 *vt は NULL 又は fnFIE_mat_aalloc() で確保されたFMATRIXのポインタでなければなりません。[in] mode 演算モード指定。次の何れかの値を指定。
( M = a->row, N = a->col, K = min(M,N), L = max(M,N) とおく )- 0: full SVD ( *u は MxM 行列, *vt は NxN 行列, *sigma の次元は L )
(*sigma)->v[K] から (*sigma)->v[L-1] は常にゼロになります。 - 1: M<=N の時、full SVD ( mode=0 の場合と一緒 ) M>N の時、 economy SVD ( u は MxK 行列, vt は KxN 行列, *sigma の次元は L ) (*sigma)->v[K] から (*sigma)->v[L-1] は常にゼロになります。
- 2: economy SVD ( u は MxK 行列, vt は KxN 行列, *sigma の次元は K )
[in] rcond ランク計算時の閾値設定
ランク計算時に 特異値 sigma[i] <= rcond*sigma[0] の値をゼロと見なします。
rcond<0.0 の値が指定されたときは、max(sigma) * eps の値を使用します。
rank にNULLが指定された場合は本パラメータは使用されません。[out] rank ランクの値
不要な場合はNULLを指定してください。 - 0: full SVD ( *u は MxM 行列, *vt は NxN 行列, *sigma の次元は L )
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
| INT FVALGAPI fnFIE_mat_chol | ( | FMATRIX * | a, | |
| CHAR * | uplo | |||
| ) |
![[[OSS]]](oss.png) 行列のコレスキー分解
行列のコレスキー分解
対称正定値行列 A のコレスキー分解を行います。
コレスキー分解は次のように与えられます。
![\[ A = \left\{ \begin{array}{ll} U^T U, & \mathrm{if} \,\,\, uplo = 'U' \\ L L^T, & \mathrm{if} \,\,\, uplo = 'L' \end{array} \right. \]](form_1028.png)
ここで 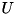 は上三角行列で
は上三角行列で 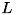 は下三角行列です。
は下三角行列です。
求められた行列は、元の行列 A に上書きされるので、元の行列が必要な場合は、 あらかじめコピーを取っておいてください。
- 覚え書き:
- 本関数では LAPACK の DPOTRF を使用して分解を行います。
- 引数:
-
[in,out] a 入力時、分解を行う行列A. - UPLO = 'U'のとき、A の上三角部に 行列Aの上三角部を格納する。 このとき、A の下三角部は参照されない。
- UPLO = 'L'のとき、A の下三角部に 行列Aの下三角部を格納する。 このとき、A の上三角部は参照されない。
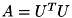 または
または 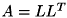 から得られた U または L が格納される。 U が格納された場合、下三角部の要素は 0 となる。 L が格納された場合、上三角部の要素は 0 となる。
から得られた U または L が格納される。 U が格納された場合、下三角部の要素は 0 となる。 L が格納された場合、上三角部の要素は 0 となる。[in] uplo - 'U': Aの上三角部に値が格納されている
- 'L': Aの下三角部に値が格納されている
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータエラー F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 行列をセット a->m[0][0] = 4.16; a->m[0][1] = -3.12; a->m[0][2] = 0.56; a->m[0][3] = -0.10; a->m[1][0] = -3.12; a->m[1][1] = 5.03; a->m[1][2] = -0.83; a->m[1][3] = 1.18; a->m[2][0] = 0.56; a->m[2][1] = -0.83; a->m[2][2] = 0.76; a->m[2][3] = 0.34; a->m[3][0] = -0.10; a->m[3][1] = 1.18; a->m[3][2] = 0.34; a->m[3][3] = 1.18; printf( "a =\n" ); mat_print( a ); fnFIE_mat_chol( a, "U" ); printf( "chol(a,\"U\") =\n" ); mat_print( a ); // 行列をセット a->m[0][0] = 4.16; a->m[0][1] = -3.12; a->m[0][2] = 0.56; a->m[0][3] = -0.10; a->m[1][0] = -3.12; a->m[1][1] = 5.03; a->m[1][2] = -0.83; a->m[1][3] = 1.18; a->m[2][0] = 0.56; a->m[2][1] = -0.83; a->m[2][2] = 0.76; a->m[2][3] = 0.34; a->m[3][0] = -0.10; a->m[3][1] = 1.18; a->m[3][2] = 0.34; a->m[3][3] = 1.18; fnFIE_mat_chol( a, "L" ); printf( "chol(a,\"L\") =\n" ); mat_print( a ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +4.160000e+000 -3.120000e+000 +5.600000e-001 -1.000000e-001 ] [ -3.120000e+000 +5.030000e+000 -8.300000e-001 +1.180000e+000 ] [ +5.600000e-001 -8.300000e-001 +7.600000e-001 +3.400000e-001 ] [ -1.000000e-001 +1.180000e+000 +3.400000e-001 +1.180000e+000 ] chol(a,"U") = [ +2.039608e+000 -1.529706e+000 +2.745626e-001 -4.902903e-002 ] [ +0.000000e+000 +1.640122e+000 -2.499814e-001 +6.737304e-001 ] [ +0.000000e+000 +0.000000e+000 +7.887488e-001 +6.616576e-001 ] [ +0.000000e+000 +0.000000e+000 +0.000000e+000 +5.346894e-001 ] chol(a,"L") = [ +2.039608e+000 +0.000000e+000 +0.000000e+000 +0.000000e+000 ] [ -1.529706e+000 +1.640122e+000 +0.000000e+000 +0.000000e+000 ] [ +2.745626e-001 -2.499814e-001 +7.887488e-001 +0.000000e+000 ] [ -4.902903e-002 +6.737304e-001 +6.616576e-001 +5.346894e-001 ] */
| INT FVALGAPI fnFIE_mat_lu | ( | FMATRIX * | a, | |
| INT * | pivot | |||
| ) |
![[[OSS]]](oss.png) 行列のLU分解
行列のLU分解
MxN行列 A を行交換による部分軸選択を用いてLU分解します。
LU分解は次のように与えられます。
![\[ P A = L U \]](form_1031.png)
ここで 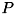 は置換行列、
は置換行列、 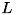 は単位対角要素を持つ下三角行列(m>nのとき下台形行列)、
は単位対角要素を持つ下三角行列(m>nのとき下台形行列)、 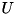 は上三角行列(m<nのとき上台形行列)です。
は上三角行列(m<nのとき上台形行列)です。
F_ERR_CALC_IMPOSSIBLE エラーが返されたとき、分解は正常に終了し a と pivot には値が格納されていますが、因子Uが特異行列となっています。 このため、この分解結果を用いて連立方程式の解を求めようとした場合には ゼロ除算が発生してしまうため、注意してください。
求められた行列は、元の行列 A に上書きされるので、元の行列が必要な場合は、 あらかじめコピーを取っておいてください。
- 覚え書き:
- 本関数では LAPACK の DGETRF を使用して分解を行います。
- 引数:
-
[in,out] a 入力時、分解する入力MxN行列A
出力時、三角分解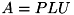 の因子LとU。 Lの単位対角要素は格納されません。
の因子LとU。 Lの単位対角要素は格納されません。 [out] pivot 軸選択用添字。min(M,N)の領域が必要です。
0 ≦i < min(M,N) に対して、行i は 行pivot[i] と交換されています。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータエラー F_ERR_CALC_IMPOSSIBLE 分解は正常に終了したが、U が特異になった F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" #include "oal_aloc.h" //メモリ管理 static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; FMATRIX *l=NULL, *u=NULL, *p=NULL; INT *pivot=NULL; INT i, j; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 3 ); // 4x3行列 A を確保 u = fnFIE_mat_aalloc( 3, 3 ); // min(M,N) x N 行列 U を確保 l = fnFIE_mat_aalloc( 4, 3 ); // M x min(M,N) 行列 L を確保 p = fnFIE_mat_aalloc( 4, 4 ); // max(M,N) x max(M,N)行列 P を確保 pivot = (INT*)fnOAL_malloc( sizeof(INT)*3 ); // min(M,N) (=3)配列を確保 // 行列をセット a->m[0][0] = 1.0; a->m[0][1] = 2.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] = 5.0; a->m[1][2] = 6.0; a->m[2][0] = 7.0; a->m[2][1] = 8.0; a->m[2][2] = 9.0; a->m[3][0] =10.0; a->m[3][1] =11.0; a->m[3][2] = 13.0; printf( "a =\n" ); mat_print( a ); // LU分解の実行 fnFIE_mat_lu( a, pivot ); printf( "lu(a) =\n" ); mat_print( a ); printf( "pivot = \n " ); for( i=0; i<3; i++ ) printf( "%d, ", pivot[i] ); printf("\n\n"); fnFIE_mat_eye( l ); fnFIE_mat_zeros( u ); fnFIE_mat_eye( p ); // Uを取り出す。 for( j=0; j<3; j++ ) for( i=0; i<3; i++ ) if( j<=i ) u->m[j][i] = a->m[j][i]; // Lを取り出す。 for( j=0; j<4; j++ ) for( i=0; i<3; i++ ) if( j>i ) l->m[j][i] = a->m[j][i]; // Pを作る for( j=0; j<3; j++ ){ // swap row(j) and row(pivot[j]) of P for( i=0; i<4; i++ ){ DOUBLE tmp; tmp = p->m[j][i]; p->m[j][i] = p->m[pivot[j]][i]; p->m[pivot[j]][i] = tmp; } } // P*A=L*U が成り立つ。 printf( "l =\n" ); mat_print( l ); printf( "u =\n" ); mat_print( u ); printf( "p =\n" ); mat_print( p ); fnFIE_mat_afree( a ); fnFIE_mat_afree( l ); fnFIE_mat_afree( u ); fnFIE_mat_afree( p ); fnOAL_free( pivot ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +1.000000e+000 +2.000000e+000 +3.000000e+000 ] [ +4.000000e+000 +5.000000e+000 +6.000000e+000 ] [ +7.000000e+000 +8.000000e+000 +9.000000e+000 ] [ +1.000000e+001 +1.100000e+001 +1.300000e+001 ] lu(a) = [ +1.000000e+001 +1.100000e+001 +1.300000e+001 ] [ +1.000000e-001 +9.000000e-001 +1.700000e+000 ] [ +7.000000e-001 +3.333333e-001 -6.666667e-001 ] [ +4.000000e-001 +6.666667e-001 +5.000000e-001 ] pivot = 3, 3, 2, l = [ +1.000000e+000 +0.000000e+000 +0.000000e+000 ] [ +1.000000e-001 +1.000000e+000 +0.000000e+000 ] [ +7.000000e-001 +3.333333e-001 +1.000000e+000 ] [ +4.000000e-001 +6.666667e-001 +5.000000e-001 ] u = [ +1.000000e+001 +1.100000e+001 +1.300000e+001 ] [ +0.000000e+000 +9.000000e-001 +1.700000e+000 ] [ +0.000000e+000 +0.000000e+000 -6.666667e-001 ] p = [ +0.000000e+000 +0.000000e+000 +0.000000e+000 +1.000000e+000 ] [ +1.000000e+000 +0.000000e+000 +0.000000e+000 +0.000000e+000 ] [ +0.000000e+000 +0.000000e+000 +1.000000e+000 +0.000000e+000 ] [ +0.000000e+000 +1.000000e+000 +0.000000e+000 +0.000000e+000 ] */
![[[OSS]]](oss.png) 行列のQR分解
行列のQR分解
MxN行列 A をQR分解します。
QR分解は次のように与えられます。
![\[ A = Q R \]](form_1034.png)
ここで 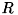 はMxNの上三角行列(M<Nのとき、上台形行列)、
はMxNの上三角行列(M<Nのとき、上台形行列)、 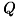 はMxMの直交行列です。
はMxMの直交行列です。
行列のサイズが同じならば、 Q または R と A は同じポインタを渡すことが出来ます。
- 覚え書き:
- 本関数では LAPACK の DGEQRF,DORGQR を使用して分解を行います。
- 引数:
-
[in] a 分解を行う MxN行列A. [out] q MxMの直交行列Q [out] r MxNの三角行列R
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; FMATRIX *q=NULL, *r=NULL; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 4 ); // M=3, N=4 の MxN 行列 A を確保 q = fnFIE_mat_aalloc( 3, 3 ); // MxM 行列 Q を確保 r = fnFIE_mat_aalloc( 3, 4 ); // MxN 行列 R を確保 // 行列をセット a->m[0][0] = 1.0; a->m[0][1] = 4.0; a->m[0][2] = 7.0; a->m[0][3] = 10.0; a->m[1][0] = 2.0; a->m[1][1] = 5.0; a->m[1][2] = 8.0; a->m[1][3] = 11.0; a->m[2][0] = 5.0; a->m[2][1] = 6.0; a->m[2][2] = 9.0; a->m[2][3] = 13.0; printf( "a =\n" ); mat_print( a ); // QR分解の実行 fnFIE_mat_qr( a, q, r ); printf( "[q,r] = qr(a)\n" ); printf( "q = \n" ); mat_print( q ); printf( "r = \n" ); mat_print( r ); fnFIE_mat_afree( a ); fnFIE_mat_afree( q ); fnFIE_mat_afree( r ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +1.000000e+000 +4.000000e+000 +7.000000e+000 +1.000000e+001 ] [ +2.000000e+000 +5.000000e+000 +8.000000e+000 +1.100000e+001 ] [ +5.000000e+000 +6.000000e+000 +9.000000e+000 +1.300000e+001 ] [q,r] = qr(a) q = [ -1.825742e-001 -7.174922e-001 -6.722140e-001 ] [ -3.651484e-001 -5.853226e-001 +7.239228e-001 ] [ -9.128709e-001 +3.776275e-001 -1.551263e-001 ] r = [ -5.477226e+000 -8.033264e+000 -1.241504e+001 -1.770970e+001 ] [ +0.000000e+000 -3.530817e+000 -6.306379e+000 -8.704313e+000 ] [ +0.000000e+000 +0.000000e+000 -3.102526e-001 -7.756315e-001 ] */
![[[OSS]]](oss.png) 行列の固有値・固有ベクトル計算
行列の固有値・固有ベクトル計算
NxNの正方行列 A の固有値を計算します。 また、選択された場合、左及び右固有ベクトルも計算します。
Aの右固有ベクトル 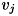 は
は
![\[ A v_j = \lambda_j v_j \]](form_1037.png)
を満たします。ここで、 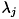 はAの固有値です。
はAの固有値です。
Aの左固有ベクトル 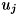 は
は
![\[ u_j^H A = \lambda_j u_j^H \]](form_1040.png)
を満たします。ここで、 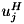 は
は 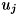 の共役転置です。
の共役転置です。
Aが対称行列の場合、v と u は等しい値となります。
- 覚え書き:
- 本関数では下記のLAPACKの関数を使用しています。
- A が対称行列の場合 : DSPEVD
- その他の場合 : DGEEV
- 引数:
-
[in] a 固有値を計算するNxN正方行列A [out] lambda 固有値配列。 N個分の領域が必要。 [out] vr Aの右固有ベクトル 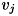
N*N個の領域が必要。
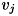 は vr[j*N]〜vr[j*(N+1)-1] に格納される。 vrが計算不要な場合はNULLを指定して下さい。
は vr[j*N]〜vr[j*(N+1)-1] に格納される。 vrが計算不要な場合はNULLを指定して下さい。 [out] vl Aの左固有ベクトル 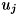
N*N個の領域が必要。
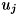 は vl[j*N]〜vl[j*(N+1)-1] に格納される。 vrが計算不要な場合はNULLを指定して下さい。
は vl[j*N]〜vl[j*(N+1)-1] に格納される。 vrが計算不要な場合はNULLを指定して下さい。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータエラー F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" #include "oal_aloc.h" //メモリ管理 static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; FCOMPLEX *lambda=NULL, *vr=NULL, *vl=NULL; INT i, j; INT m=2, n=2; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( m, n ); // 2x2行列 A を確保 lambda = (FCOMPLEX*)fnOAL_malloc( sizeof(FCOMPLEX)*n ); vr = (FCOMPLEX*)fnOAL_malloc( sizeof(FCOMPLEX)*n*n ); vl = (FCOMPLEX*)fnOAL_malloc( sizeof(FCOMPLEX)*n*n ); // 行列をセット a->m[0][0] = 1.0; a->m[0][1] = 2.0; a->m[1][0] = -2.0; a->m[1][1] = 2.0; printf( "a =\n" ); mat_print( a ); // 固有値計算の実行 - lambda だけ求める fnFIE_mat_eig( a, lambda, NULL, NULL ); printf( "eig(a)\n" ); printf( "lambda = \n " ); for( i=0; i<n; i++ ) printf( "%+0.6e %+0.6ei ", lambda[i].real, lambda[i].image ); printf( "\n\n" ); // 固有値計算の実行 - lambda, vr, vl を求める fnFIE_mat_eig( a, lambda, vr, vl ); printf( "eig(a)\n" ); printf( "lambda = \n " ); for( i=0; i<n; i++ ) printf( "%+0.6e %+0.6ei ", lambda[i].real, lambda[i].image ); printf( "\n" ); for( j=0; j<n; j++ ){ printf( "vr[%d] = [ ", j ); for( i=0; i<n; i++ ) printf( "%+0.6e %+0.6ei ", vr[i+n*j].real, vr[i+n*j].image ); printf( " ]\n" ); } for( j=0; j<n; j++ ){ printf( "vl[%d] = [ ", j ); for( i=0; i<n; i++ ) printf( "%+0.6e %+0.6ei ", vl[i+n*j].real, vl[i+n*j].image ); printf( " ]\n" ); } fnFIE_mat_afree( a ); fnOAL_free( lambda ); fnOAL_free( vr ); fnOAL_free( vl ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +1.000000e+000 +2.000000e+000 ] [ -2.000000e+000 +2.000000e+000 ] eig(a) lambda = +1.500000e+000 +1.936492e+000i +1.500000e+000 -1.936492e+000i eig(a) lambda = +1.500000e+000 +1.936492e+000i +1.500000e+000 -1.936492e+000i vr[0] = [ +7.071068e-001 +0.000000e+000i +1.767767e-001 +6.846532e-001i ] vr[1] = [ +7.071068e-001 -0.000000e+000i +1.767767e-001 -6.846532e-001i ] vl[0] = [ +7.071068e-001 +0.000000e+000i -1.767767e-001 +6.846532e-001i ] vl[1] = [ +7.071068e-001 -0.000000e+000i -1.767767e-001 -6.846532e-001i ] */
| INT FVALGAPI fnFIE_mat_cond | ( | const FMATRIX * | a, | |
| INT | type, | |||
| DOUBLE * | cond | |||
| ) |
![[[OSS]]](oss.png) 行列の条件数計算
行列の条件数計算
MxN行列 A の条件数を計算します。
type == 2 のとき、本関数はSVDの最大値と最小値の比で定義される、 2ノルム条件数を返します。
その他の場合、本関数は下式にて定義される type ノルム条件数を返します。
![\[ \|a\|_{type} * \|a^{-1}\|_{type} \]](form_1042.png)
type != 2 のとき、入力行列Aは正方行列でなければいけません。
- 覚え書き:
- 本関数では下記のLAPACKの関数を使用しています。
- 1/infinity/frobenius norm 条件数 : DLANGE, DGETRI, DGETRF
- 2-norm 条件数: DGESDD
- 引数:
-
[in] a 固有値を計算するMxN行列A [in] type 求める条件数の種類 - 1 : 1-norm 条件数
- 2 : 2-norm 条件数
- I32_MAX : infinity norm 条件数
- -1 : Frobenius norm 条件数
[out] cond 条件数
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM 不正なパラメータが渡された F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 入力値をセット fnFIE_mat_rand( a ); printf( "a =\n" ); mat_print( a ); // L1-norm fnFIE_mat_cond( a, 1, &d ); printf( "cond(a, 1) =\n" ); printf( " %+0.6e\n\n", d ); // L2-norm fnFIE_mat_cond( a, 2, &d ); printf( "cond(a, 2) =\n" ); printf( " %+0.6e\n\n", d ); // INF-norm fnFIE_mat_cond( a, INT_MAX, &d ); printf( "cond(a, inf) =\n" ); printf( " %+0.6e\n\n", d ); // frobenius-norm fnFIE_mat_cond( a, -1, &d ); printf( "cond(a, fro) =\n" ); printf( " %+0.6e\n\n", d ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +2.509236e-001 +6.805727e-001 +4.609582e-002 +3.209734e-001 ] [ +6.768162e-001 +1.553593e-001 +4.346949e-002 +6.005672e-001 ] [ +1.164237e-001 +9.243582e-001 +6.038657e-001 +7.878644e-001 ] [ +1.909307e-001 +7.638308e-001 +6.685157e-001 +7.029740e-001 ] cond(a, 1) = +3.902937e+001 cond(a, 2) = +2.554015e+001 cond(a, inf) = +3.643580e+001 cond(a, fro) = +2.824149e+001 */
| INT FVALGAPI fnFIE_mat_rcond | ( | const FMATRIX * | a, | |
| DOUBLE * | rcond | |||
| ) |
![[[OSS]]](oss.png) 行列の条件数の逆数計算
行列の条件数の逆数計算
LAPACKの条件判定ルーチンを使用して正方行列Aの1ノルム条件数の逆数を 計算します。行列A の条件が良い場合 rcond は1.0に近くなり、 条件が悪い場合には rcond は 0.0 に近くなります。
評価値は 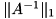 に対して得られ、条件数の逆数は 下式にて計算されます。
に対して得られ、条件数の逆数は 下式にて計算されます。
![\[ RCOND = \frac{1}{\|A\|_1 * \|A^{-1}\|_1} \]](form_1044.png)
- 覚え書き:
- 本関数では下記のLAPACKの関数を使用しています。
DLANGE, DGETRF, DGECON
- 引数:
-
[in] a 条件数の逆数を計算するNxN正方行列A [out] rcond 条件数の逆数
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL; DOUBLE d; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 4, 4 ); // 4x4行列 a を確保 // 入力値をセット fnFIE_mat_rand( a ); printf( "a =\n" ); mat_print( a ); fnFIE_mat_rcond( a, &d ); printf( "rcond(a) =\n" ); printf( " %+0.6e\n\n", d ); fnFIE_mat_afree( a ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 a = [ +2.509236e-001 +6.805727e-001 +4.609582e-002 +3.209734e-001 ] [ +6.768162e-001 +1.553593e-001 +4.346949e-002 +6.005672e-001 ] [ +1.164237e-001 +9.243582e-001 +6.038657e-001 +7.878644e-001 ] [ +1.909307e-001 +7.638308e-001 +6.685157e-001 +7.029740e-001 ] rcond(a) = +2.562173e-002 */
![[[OSS]]](oss.png) 行列の逆行列計算(LAPACK使用)
行列の逆行列計算(LAPACK使用)
NxN行列 A の逆行列をLU分解を使用して計算します。
A と Ai に同じポインタを渡すことが出来ます。
- 覚え書き:
- 本関数では LAPACK の DGETRF と DGETRI を使用して分解を行います。
- 引数:
-
[in] a 逆行列を計算するNxN行列A [out] ai A の逆行列 [out] det A の行列式
計算不要な場合はNULLを指定可能。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE LU分解の結果、因子Uが特異になったため計算出来なかった。 F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } INT main() { FMATRIX *a=NULL, *b=NULL; DOUBLE det; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 a を確保 b = fnFIE_mat_aalloc( 3, 3 ); // 3x3行列 b を確保 // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; printf( "a =\n" ); mat_print( a ); // a を上書きして a^-1 を計算 fnFIE_mat_inverse( a ); printf( "fnFIE_mat_inverse()\n" ); printf( "a^-1 = \n" ); mat_print( a ); // 入力値をセット a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; // a^-1 => b を計算 // inverse2 は a の内容を破壊するので注意 fnFIE_mat_inverse2( a, b, &det ); printf( "fnFIE_mat_inverse2()\n" ); printf( "det(a) = %f\n", det ); printf( "a^-1 = \n" ); mat_print( b ); a->m[0][0] = 1.0; a->m[0][1] = 3.0; a->m[0][2] = 3.0; a->m[1][0] = 4.0; a->m[1][1] =-2.0; a->m[1][2] = 1.0; a->m[2][0] = 2.0; a->m[2][1] = 5.0; a->m[2][2] =-1.0; // a^-1 => b を計算 fnFIE_mat_inverse3( a, b, &det ); printf( "fnFIE_mat_inverse3()\n" ); printf( "det(a) = %f\n", det ); printf( "a^-1 = \n" ); mat_print( b ); fnFIE_mat_afree( a ); fnFIE_mat_afree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果 a = [ +1.000000e+000 +3.000000e+000 +3.000000e+000 ] [ +4.000000e+000 -2.000000e+000 +1.000000e+000 ] [ +2.000000e+000 +5.000000e+000 -1.000000e+000 ] fnFIE_mat_inverse() a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] fnFIE_mat_inverse2() det(a) = 87.000000 a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] fnFIE_mat_inverse3() det(a) = 87.000000 a^-1 = [ -3.448276e-002 +2.068966e-001 +1.034483e-001 ] [ +6.896552e-002 -8.045977e-002 +1.264368e-001 ] [ +2.758621e-001 +1.149425e-002 -1.609195e-001 ] */
| INT FVALGAPI fnFIE_mat_pseudo_inverse | ( | const FMATRIX * | a, | |
| FMATRIX * | ai, | |||
| DOUBLE | threshold, | |||
| INT * | rank | |||
| ) |
![[[OSS]]](oss.png) 行列の擬似逆行列計算(LAPACK使用)
行列の擬似逆行列計算(LAPACK使用)
MxN行列 a の擬似逆行列を計算します。
- 覚え書き:
- 本関数では fnFIE_mat_svd2() を使用して分解を行います。
- 引数:
-
[in] a 擬似逆行列を計算する行列(サイズ:MxN) [out] ai a の擬似逆行列(サイズ:NxM) [in] threshold 擬似行列計算する際に特異値の閾値 [out] rank a のランク。NULLを指定可能。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_CALC_IMPOSSIBLE 計算不能エラー F_ERR_INVALID_PARAM パラメータエラー F_ERR_NOMEMORY メモリ不足エラー F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
| INT FVALGAPI fnFIE_mat_linsolve | ( | const FMATRIX * | a, | |
| FVECTOR * | x, | |||
| const FVECTOR * | b, | |||
| INT | method, | |||
| DOUBLE * | residual, | |||
| DOUBLE | rcond, | |||
| INT * | rank | |||
| ) |
![[[OSS]]](oss.png) 連立一次方程式の計算
連立一次方程式の計算
過剰、または過小定義の連立一次方程式  を解きます。
を解きます。
- a->row > a->col の場合:
過小定義式![\[ \bf{A} \bf{x} = \bf{b} \]](form_1046.png)
の最小ノルム解を求めます。
- a->row ≦ a->col の場合:
最小二乗問題![\[ \min \| \bf{b} - \bf{A}\bf{x} \| \]](form_1047.png)
を解いて、過剰定義連立方程式の最小二乗解を求め x へ出力します。 また residual には求められた x での残差二乗和
![\[ \sum (\bf{b} - \bf{A}\bf{x})^2 \]](form_1048.png)
が返されます。
a, b, x の次元が不正な場合は F_ERR_INVALID_PARAM を返します。 また b と x の次元が同じでも、同じポインタを渡すことは出来ません。 この様な指定をした場合は正しい結果を得られません。
- 解法選択
- 本ルーチンは method パラメータにより解法を選択できます。
- medthod = 0 の場合:
本ルーチンは QR または LQ 分解を用いた手法により問題を解きます。 行列 はフルランクでなければいけません。
はフルランクでなければいけません。 - medthod = 1 の場合:
本ルーチンは SVD を用いた手法により問題を解きます。 行列 はランク落ちしていてもかまいません。
はランク落ちしていてもかまいません。 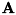 の有効なランクは、最大特異値 と rcond の積 よりも小さな特異値をゼロと見なすことにより決定されます。
の有効なランクは、最大特異値 と rcond の積 よりも小さな特異値をゼロと見なすことにより決定されます。
- medthod = 0 の場合:
- 覚え書き:
- 本関数では LAPACK の DGELSD, DGELS, ILAENV を使用しています。
- 引数:
-
[in] a MxN 係数行列 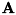
[out] x 解ベクトル 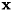
x の次元はNでなければいけません。[in] b 右辺ベクトル 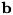
b の次元はMでなければいけません。[in] method 解法。下記のいずれかを指定
- 0 : QR または LQ 分解を使用した手法により計算
- 1 : SVD を使用した手法により計算
[out] residual 誤差二乗和
a->row <= a->col の場合、本パラメータは使用されません。
不要な場合はNULLを指定してください。[in] rcond ゼロ判定閾値
method != 1 の場合本パラメータは無視されます。
ランク計算時に 特異値 sigma[i] <= rcond*sigma[0] の値をゼロと見なします。
rcond<0.0 の値が指定されたときは、max(sigma) * eps の値を使用します。
[out] rank 行列 a のランク
不要な場合はNULLを指定してください。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NOMEMORY メモリ不足エラー F_ERR_CALC_IMPOSSIBLE 計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- example code
// エラー処理は省略しているので注意して下さい。 #include <stdio.h> #include "fie.h" static VOID mat_print( FMATRIX *a ) { INT i,j; for( j=0; j<a->row; j++ ){ printf( " [ " ); for( i=0; i<a->col; i++ ){ printf( "%+0.6e ", a->m[j][i] ); } printf( "]\n" ); } printf( "\n" ); } static VOID vect_print( FVECTOR *v ) { INT i; printf( " [ " ); for( i=0; i<v->dim; i++ ){ printf( "%+0.6e ", v->v[i] ); } printf( "]\n" ); printf( "\n" ); } INT main() { FMATRIX *a=NULL; FVECTOR *x=NULL, *b=NULL; DOUBLE residual; INT rank; // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); a = fnFIE_mat_aalloc( 5, 3 ); // 5x3行列 A を確保 x = fnFIE_mat_valloc( 3 ); // 次元3のベクトル x を確保 b = fnFIE_mat_valloc( 5 ); // 次元5のベクトル b を確保 // 入力値をセット // // A * x = b // |4 5 8| |x1| |38| // |3 2 1| |x2| = |10| // |4 5 6| |x3| |32| // |1 3 -1| | 4| // |9 6 2| |27| a->m[0][0] = 4; a->m[0][1] = 5; a->m[0][2] = 8; b->v[0] = 38; a->m[1][0] = 3; a->m[1][1] = 2; a->m[1][2] = 1; b->v[1] = 10; a->m[2][0] = 4; a->m[2][1] = 5; a->m[2][2] = 6; b->v[2] = 32; a->m[3][0] = 1; a->m[3][1] = 3; a->m[3][2] = -1; b->v[3] = 4; a->m[4][0] = 9; a->m[4][1] = 6; a->m[4][2] = 2; b->v[4] = 27; // min|| b - A * x || を解く fnFIE_mat_linsolve( a, x, b, 1/*SVD*/, &residual, 1e-10/*rcond*/, &rank ); printf( "A =\n" ); mat_print( a ); printf( "x =\n" ); vect_print( x ); printf( "b =\n" ); vect_print( b ); printf( "rank of A=%d\n", rank ); printf( "residual=%e\n", residual ); fnFIE_mat_afree( a ); fnFIE_mat_vfree( x ); fnFIE_mat_vfree( b ); // 終了処理 fnFIE_teardown(); return 0; } /* 結果例 A = [ +4.000000e+000 +5.000000e+000 +8.000000e+000 ] [ +3.000000e+000 +2.000000e+000 +1.000000e+000 ] [ +4.000000e+000 +5.000000e+000 +6.000000e+000 ] [ +1.000000e+000 +3.000000e+000 -1.000000e+000 ] [ +9.000000e+000 +6.000000e+000 +2.000000e+000 ] x = [ +1.000000e+000 +2.000000e+000 +3.000000e+000 ] b = [ +3.800000e+001 +1.000000e+001 +3.200000e+001 +4.000000e+000 +2.700000e+001 ] rank of A=3 residual=-5.329071e-015 */
| INT FVALGAPI fnFIE_mat_linsolve2 | ( | const FMATRIX * | a, | |
| FMATRIX * | x, | |||
| const FMATRIX * | b, | |||
| INT | method, | |||
| DOUBLE * | residuals, | |||
| DOUBLE | rcond, | |||
| INT * | rank | |||
| ) |
![[[OSS]]](oss.png) 連立一次方程式の計算
連立一次方程式の計算
過剰、または過小定義の連立一次方程式 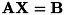 を解きます。
を解きます。
fnFIE_mat_linsolve() との違いは、解と右辺に行列を入力し、 NRHS個の連立方程式を同時に解けるようになっている点です。
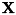 の i 列目の列ベクトルを
の i 列目の列ベクトルを 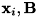 の i 列目の列ベクトルを
の i 列目の列ベクトルを 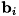 とします (0 <= i < NRHS)。
とします (0 <= i < NRHS)。
- a->row > a->col の場合:
全ての i について、過小定義式![\[ {\bf A} {\bf x}_i = {\bf b}_i \]](form_1056.png)
の最小ノルム解を求めます。
- a->row ≦ a->col の場合:
最小二乗問題![\[ \min \| {\bf b}_i - {\bf A} {\bf x}_i \| \]](form_1057.png)
を解いて、過剰定義連立方程式の最小二乗解を求め x へ出力します。 また residuals には求められた x での列ごとの残差二乗和が返されます。 より形式的には、residuals[i] には行列
![\[ (\bf{B} - \bf{A}\bf{X})^T (\bf{B} - \bf{A}\bf{X}) \]](form_1058.png)
の i 行 i 列目の成分が格納されます (0 <= i < NRHS)。
a, b, x の次元が不正な場合は F_ERR_INVALID_PARAM を返します。 また b と x の次元が同じでも、同じポインタを渡すことは出来ません。 この様な指定をした場合は正しい結果を得られません。
- 解法選択
- 本ルーチンは method パラメータにより解法を選択できます。
- medthod = 0 の場合:
本ルーチンは QR または LQ 分解を用いた手法により問題を解きます。 行列 はフルランクでなければいけません。
はフルランクでなければいけません。 - medthod = 1 の場合:
本ルーチンは SVD を用いた手法により問題を解きます。 行列 はランク落ちしていてもかまいません。
はランク落ちしていてもかまいません。  の有効なランクは、最大特異値 と rcond の積 よりも小さな特異値をゼロと見なすことにより決定されます。
の有効なランクは、最大特異値 と rcond の積 よりも小さな特異値をゼロと見なすことにより決定されます。
- medthod = 0 の場合:
- 覚え書き:
- 本関数では LAPACK の DGELSD, DGELS, ILAENV を使用しています。
- 引数:
-
[in] a MxN 係数行列 
[out] x NxNRHS 解行列 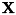
[in] b MxNRHS 右辺行列 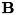
[in] method 解法。下記のいずれかを指定
- 0 : QR または LQ 分解を使用した手法により計算
- 1 : SVD を使用した手法により計算
[out] residuals 誤差二乗和
a->row <= a->col の場合、本パラメータは使用されません。
不要な場合はNULLを指定してください。
そうでない場合は、NRHS * sizeof(DOUBLE) byte のバッファが必要です。
[in] rcond ゼロ判定閾値
method != 1 の場合本パラメータは無視されます。
ランク計算時に 特異値 sigma[i] <= rcond*sigma[0] の値をゼロと見なします。
rcond<0.0 の値が指定されたときは、max(sigma) * eps の値を使用します。
[out] rank 行列 a のランク
不要な場合はNULLを指定してください。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_NOMEMORY メモリ不足エラー F_ERR_CALC_IMPOSSIBLE 計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー