説明
[決定木]

決定木について

決定木は、データの特徴量を用いた簡単なルールで分岐を作り、対象となる特徴空間を分割することを通じて 識別を行う、決定理論やデータマイニングなどで広く用いられるモデルです。 決定木は、出力として以下のような木構造の分類ルール(ここでは例としてX, Yの座標に対応する領域の分類)を出力します。

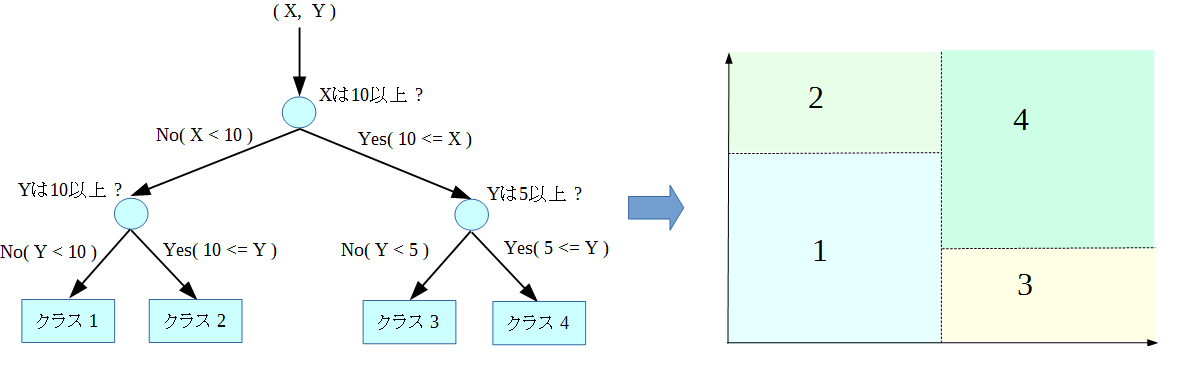
fie_ml_dtree.png

決定木の各内節ノードは、入力データ中のどのデータを用いて、どのような判断(分岐)をするかを示し、 末端の葉ノードは、これ以上分岐をする必要がない状態を意味し、最終的な分類を意味します。決定木は、 入力に対して逐次的なテストを行い、最終的な分類を決定するテストルールの構造、もしくはIF-ELSE形式の 条件文の集まりを示したものともいえます。
機械学習における決定木は、与えられた教師データ群を基にした適切な分類ルールを作成する処理となります。

カテゴリ属性と数値属性の扱い

決定木では、入力の特徴ベクトルの属性として、「数値属性」と「カテゴリ属性」を扱うことができます。

数値属性とは、特徴ベクトルの各値が連続変数、つまり2つの異なる値が数値として比較可能なものであることを意味します。 例として、"画素の濃度"や"対象物の面積"のように、具体的に数値として観測されたものが当たります。

カテゴリ属性とは、特徴ベクトルの各値が、離散的なクラスラベルを示す値であることを意味します。 例として「矩形 = 0」「円 = 1」「楕円 = 2」のように、特定の属性を数値と対応させ、その属性を示す ラベルとしたものが当たります。

なお、カテゴリ属性のベクトルを扱う場合、特徴ベクトルの各値は全て整数値である必要があります。

決定木の作成について

機械学習の分野における決定木の基本的な処理は以下のようになります。

1：木の根ノード(ルートノード)に全教師データを対応付ける

2：木のノードと対応付けされた教師データが停止条件を満たすかを確認する

3：木のすべてのノードが停止条件を満たすまで、2の処理を再帰的に繰り返す

この処理を具体的に行うには、「適応可能な分岐ルールの集合」「分岐の選択基準」「停止条件」を決める必要があります。 本ライブラリでは、参考文献[1]にて紹介されているアルゴリズム(CART法)を実装しており、各条件は以下のようになります。

分岐ルール集合
分岐ルール集合、つまりノードに対応付けされた教師データを分割するための基準の集合は、特徴ベクトルがカテゴリ属性か 数値属性かで違いはありますが、基本的には教師データ内の網羅的な探索で決定します。 なお、分岐ルールの内容からわかるように、本ライブラリでの決定木は二分木(葉ノード以外のノードは全て子ノードを2つ持つ) 構造となります。
分岐ルールの選択基準
どの分岐ルールが対象ノードにおける最適な分岐規則とするかの基準には、ジニ係数(Gini index)が 用いられます。ジニ係数は、経済学の分野では所得格差を示す尺度として用いられており、データのばらつき具合を示す数値に なります。つまり、ある基準で教師データを二つに分割したとき、分割前に比べてどれだけデータの純度が向上したか (データのばらつきが低減したか)を選択の基準とし、最も純度が向上できるものを採用します。
停止条件
以下に示すいずれかの条件を満たしたときに、ノードの再帰的処理(ノードの成長)が停止します。
  • 対象のノードの深さが、ユーザが指定した最大値に達したとき
  • 対象のノードに対応付けられた教師データの数が、ユーザが指定した最小値以下になったとき
  • 対象のノードに対応付けられた教師データが、全て同じラベルをもつデータとなったとき

枝刈り

一般的に決定木をより深く、細分化して学習をさせた場合、教師データに対する識別性能は向上します。 しかし、複雑化した決定木は、入力された教師データに対して過剰に適合しているため、教師データには 現れない未知のデータに対する分類性能(汎化性能)は逆に低下してしまいます。 また、教師データ内に含まれるノイズや、データ上の偏りなど、本来なら学習すべきではないものまで 学習をしてしまうことで、決定木のもつ識別性能は低下します。(このような状況を過学習 = Over-Fitting といいます)

このような状況に対して、決定木では、不要と思われる分岐を削除する枝刈り(Pruning)を行うことで対応をします。 枝刈りには、木の成長途中でその分岐の信頼性を評価して成長を止める事前枝刈り(Pre-Pruning)と、 木を一度最大まで構築した後で、過剰と判断した分岐を削除していく事後枝刈り(Post-Pruning)が知られていますが、 本ライブラリでは、より効果が高いとされる事後枝刈りを採用しています。

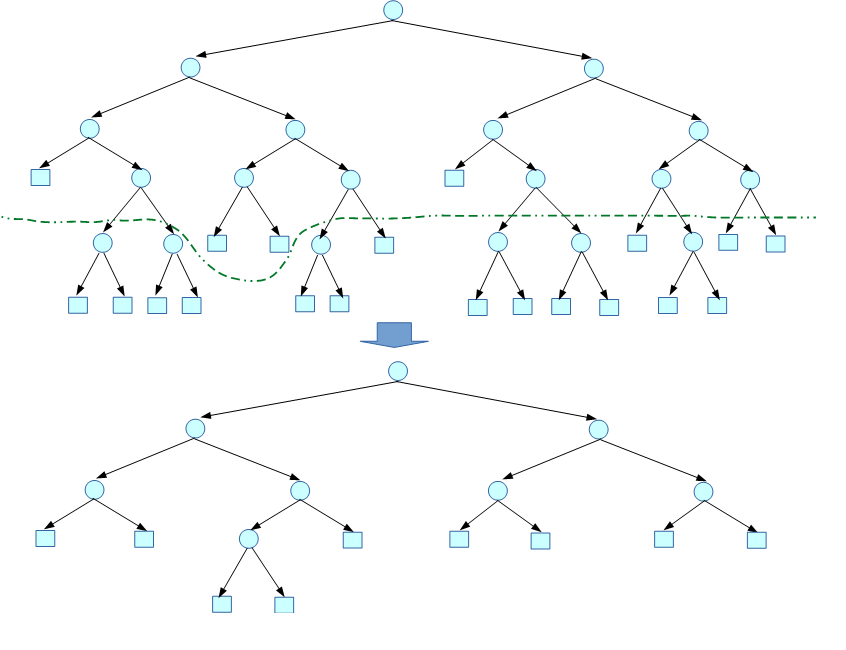
fie_ml_dtree_pruning.png

本ライブラリでは、複数の枝刈り手法を提供しますが、基本的には「交差検証(Cross-validation)」による 試行錯誤的な枝刈りとなります。交差検証とは、与えられた教師データを複数のブロックに等分割し、ある一つの ブロックを誤識別率などの精度を測るためのテスト検証用として残し、残りを学習用データとして用いるというものです。 これを、テスト用のブロックを変更しながら繰り返し行い、得られたk個の精度から最終的な結果を取得します。 教師データを分割するブロックをk個とする交差検証を、k分割交差検証(k-fold Cross-validation)と呼びます。

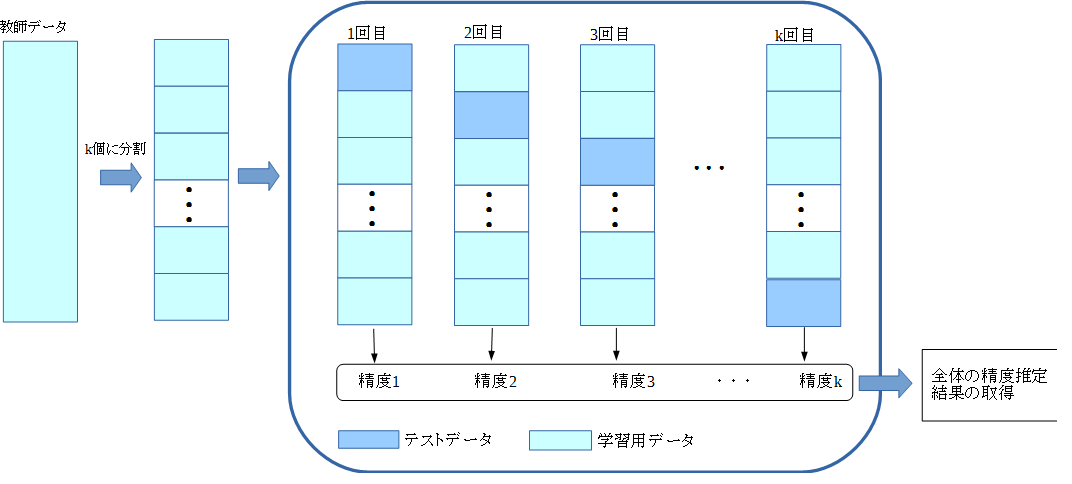
fie_ml_dtree_k_cv.png

提供する枝刈りの手法は以下のものになります。

エラー減少枝刈り
エラー減少枝刈りは、k分割交差検証を用いた、単純な枝刈りの手法です。教師データをk個のブロックに分割し、 一つのブロックをテスト用データとして残し、残りのk-1個のブロックで決定木を最大まで成長させます。 そして、テスト用データを用いて、以下の処理を繰り返します。

この一連の手続きをテスト用データを変えながら繰り返し、k本の枝刈り済の木を取得します。そしてその中で最も 誤識別率の小さい木を最終的な決定木として出力します。
エラー減少枝刈りは、交差検証による誤識別率の精度という観点で、正確でかつ最小の木を得ることができます。 しかし、与えられる教師データ数が十分ではない場合、逆に得られる決定木の性能が悪化する可能性があります。 また、得られた決定木は、本質的には全ての教師データを用いて学習した木ではないという欠点もあります。
コスト複雑度枝刈り
コスト複雑度枝刈りは、参考文献[1]にて紹介された枝刈りの手法です。この手法は、まず与えられた教師データを 全て用いて、決定木を最大まで成長させます。その後、この決定木の各内点ノードをルートとする部分木に対して、 以下のようなエラーコストの評価式でコストを評価します。

\[ R_{\alpha}(T_{t}) = R(T_{t}) + \alpha |{T_{t_{leaf}}}| \]

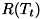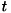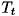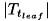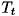ここで、$R(T_{t})$は決定木のある内点ノード$t$をノードとする部分木$T_{t}$のエラーコスト、 $|{T_{t_{leaf}}}|$は部分木$T_{t}$の葉ノードの数、そして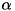$\alpha$は木の複雑さをどの程度考慮するかを 決める重み係数となります。そして、この評価式で得られた値が、一定の閾値を越えた部分木を枝刈りします。 (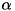$\alpha$が小さければ、あまり枝刈りは行われず、多くのノード数を持つ木になります。 逆に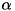$\alpha$が大きければ、多くの部分木が削除され、ノード数が少なくなります)
最適な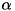$\alpha$の選択(=最適な枝刈り)は、k分割交差検証によって決定します。つまり、k本の木を作成し、 その各木に対して、ある係数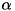$\alpha$で実際に枝刈りを行います。そして、テスト用データで誤識別率を算出し、 その平均値が最も低いときの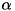$\alpha$を採用します。
この手法は、試行錯誤的な処理を繰り返すので、処理にやや時間を要します。また、処理に必要とするメモリ量も比較的 多くなります。しかし、与えられた教師データが十分利用できるときに、有効に働く処理でもあります。
コスト複雑度枝刈り(1-SEルール使用)
1-SEルールを用いた枝刈りは、コスト複雑度枝刈りと同じく[1]にて紹介された手法です。 この手法は、基本的にはコスト複雑度枝刈りと同じものになります。通常のコスト複雑度枝刈りとの違いは、 最良の枝刈りの決定を決定する基準です。
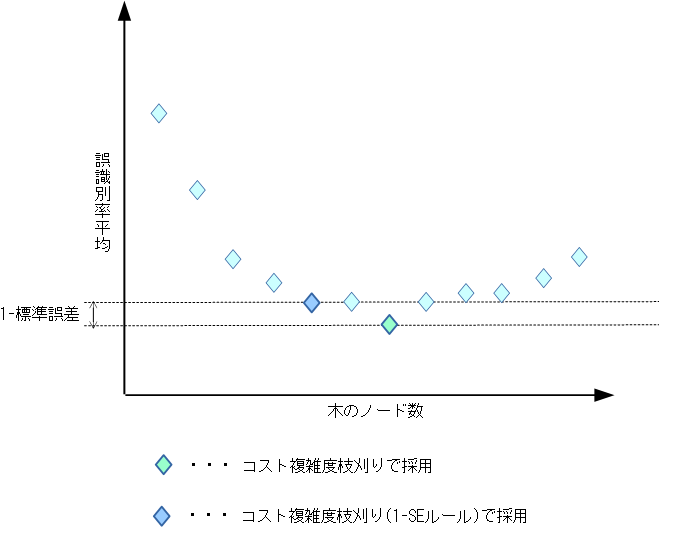
コスト複雑度枝刈りの場合は、k分割交差検証によるテストで、誤識別率の平均が最小となるもの最良としていますが、 1-SEルールを適応する場合は、さらに1標準誤差(1-Standart Error)を考慮にいれます。最良の木を決定する際に、 誤識別率の平均が最小となった時点での、k本の決定木における誤識別率の1標準誤差を計算します。 そして、誤識別率が(最小の誤識別率 + 1標準誤差)を満たす範囲で、 最もコンパクトなものを採用します。
fie_ml_dtree_1se.png

決定木のパラメータ

決定木で必要となるパラメータを説明します。精度の高い識別を行うためには、パラメータの調整が必要です。

木の最大の深さ
決定木が取りうる最大の深さを指定します。木のノードの深さがこの値に達した場合、そのノードの成長を 終了し、そのノードを葉ノードとします。この値を大きくすれば、より複雑で細かな分岐を行う決定木が構成されますが、 その分過学習を起こしやすくなります。なお、この値を0で指定した場合は、木の深さについては無制限に成長を続けます。
最小サンプル数
学習中、各ノードに割り当てられる教師データの最小数を指定します。分岐処理中に、対象のノードに割り当てられた 教師データのサンプル数が、この値以下になった場合、そのノードの成長を終了し、そのノードを葉ノードとします。 この値を小さくした場合は、より詳細な分割を行いますが、その分構成が複雑となり、過学習を起こしやすくなります。
交差検証数
決定木の枝刈りを行う際の、k分割交差検証の分割数(kの値)を指定します。kの値を大きくすれば、モデルの 評価がより正確となりますが、その分処理に要する時間が増大します。教師データの数にもよりますが、 おおよそ10程度が一般的とされています。なお、(交差検証の定義から明白ですが)この値は2以上でなければなりません。
枝刈りのタイプ
決定木の枝刈りのタイプを指定します。指定できるパラメータは以下のようになります。
特徴ベクトルの属性
入力された教師データの特徴ベクトルが、数値属性であるか、カテゴリ属性であるかを指定します。 数値属性を指定した場合は、教師データの各値を連続的な数値として扱います、 カテゴリ属性を指定した場合は、特徴ベクトルの各値を、離散的なラベルとして扱います。
なお、カテゴリ属性を指定する場合は、特徴ベクトルの値は全て整数値である必要があります。 そのため、小数点以下の値が含まれていた場合は、小数点以下の値は内部で強制的に切り捨てられ、 整数値に変換されます。つまり、カテゴリの区別は全て整数値部分の値のみで行われます。
事前処理
学習を開始する前に、与えられた教師データに行う前処理を指定します。 指定可能な事前処理は以下のものになり、これらは組み合わせて同時に指定可能です。
教師データの特徴ベクトルがカテゴリ属性で合った場合は、事前処理の指定は無視されます。これは以下の理由によります
  • 特徴ベクトルの値は属性を示すラベルを意味し、数値的な意味を持たない
  • カテゴリ属性の場合は、重複性は分岐を決定する上でむしろ情報となるため
また、決定木の学習では、まずは事前処理を指定せずに学習を行い、パラメータの調整で精度を上げていく事を推奨します。
学習時間
学習を行う時間の上限を秒単位で設定します。教師データの内容や、パラメータ の指定によっては、学習に極端に時間がかかる場合があります。このパラメータで学習に用いる時間の 上限を設定しておくと、学習の終了条件を満たす前であっても学習を打ち切ります。 値を0にすると、終了条件を満たすまで学習を続ける設定になります。

その他

学習結果の取得:
決定木は、分岐ルールとその木構造のつながりという、非常に単純な構造をしています。 そのため、決定木の利点の一つとして、学習した結果(判別のルールと全体の構造)が容易に理解できることがあげられます。 学習した決定木を識別に用いるだけではなく、その内部構造を解析し、どのような分岐基準が採用されているかや、 入力値に対して、どのようなテストルールを通過して出力がなされたか、などを確認することができます。
本ライブラリでは、決定木の構造を解析するためのツール関数を提供しています。
枝刈り処理時の内部処理
前述のように、本ライブラリで枝刈りを行う際には、指定パラメータ数での分割交差検証を行います。その際、 教師データに偏りがあると正確な交差検証ができない可能性があるため、内部で fnFIE_mtrand_real1() を用いた 教師データのランダムシャッフルを行っています。そのため、教師データが同じでも、出力される結果が異なる可能性が あります。
カテゴリ属性での学習時間
カテゴリ属性の教師データによる学習では、特徴ベクトルの各次元が持つカテゴリ集合を2分割する組み合わせを列挙し、 その組み合わせを網羅的に探索して分岐ルールを決定します。そのため、取り扱うカテゴリ数が増えていくと、 探索する組み合わせの数が指数的に増加し、学習に時間を要することに注意してください。
参考文献:

Documentation copyright © 2009-2024 FAST Corporation.
Generated on Fri Aug 9 16:38:48 2024 for FIEライブラリ by doxygen 1.5.6-FASTSP-p2