説明
[照度差ステレオ]
照度差ステレオについて
照度差ステレオ全般について
本ライブラリは、物体表面の法線を推定する照度差ステレオの機能を提供するライブラリです。照度差ステレオでは、カメラを固定し、 光源ベクトル が相異なる照明を用いて撮像した複数枚の画像を用います。 同じ場所でも物体表面の明るさは光源ベクトルに依存することを利用して法線を推定します。法線を利用し、物体表面の高さ、曲率を得る関数等も本ライブラリに含まれます。 本ライブラリを使用することで、見る方向によっては見つけにくい対象を強調することや、背景やテクスチャの影響を抑えた凹凸の情報を得ることができます。照度差ステレオの使い方
照度差ステレオで法線画像(normal map)やアルベド画像(albedo map)を求める場合、 fnFIE_ps_woodham() を使用します。 撮像対象(object)を固定、カメラを固定し、光源ベクトルが相異なる照明を用いて撮像した画像と光源ベクトルが複数必要です。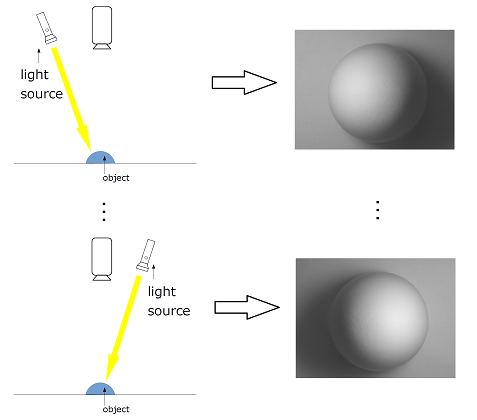
Fig1. 光源ベクトルが相異なる照明を用いて撮像した画像例
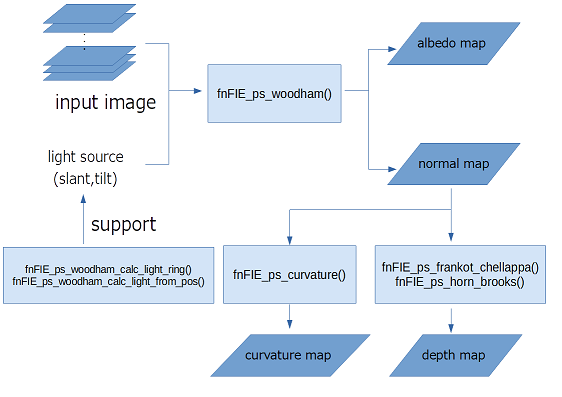
Fig2. 照度差ステレオの使い方
具体的な関数の使用方法は、サンプルコード を参照して下さい。
- 法線ベクトル、光源ベクトル
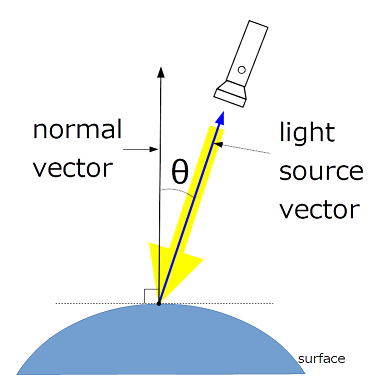
Fig3.法線ベクトル、光源ベクトル(normal vector, light source vector)
- slantとtilt
- slant:z軸と光源ベクトルがなす角(0°≦slant≦180°)
- tilt:光源ベクトルをxy平面に射影したベクトルとx軸がなす角で、x軸から時計回りの角度
です。
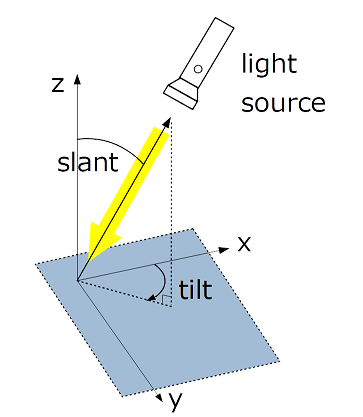
Fig4. slant, tilt
fnFIE_ps_woodham_calc_light_from_pos()
fnFIE_ps_woodham_calc_light_ring()
- 照度差ステレオモジュールで用いる座標系について
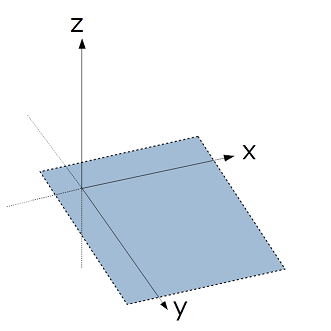
Fig5. 左手系(left-handed system)
また、撮像に用いるカメラのモデルは平行投影(orthographic projection)モデルを仮定します(Fig.6)。カメラのx,yのスケールは同じとします。座標系について、Z軸を光軸と平行にとり、X軸、Y軸は投影面(画像)の横方向と縦方向と平行にとったものとする座標系を用います。 Z軸の向きは物体からカメラの向きを正とします(Fig.7)。
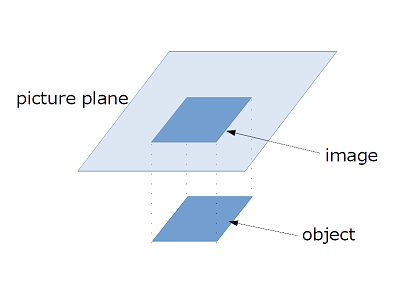
Fig6. 平行投影(orthographic projection)
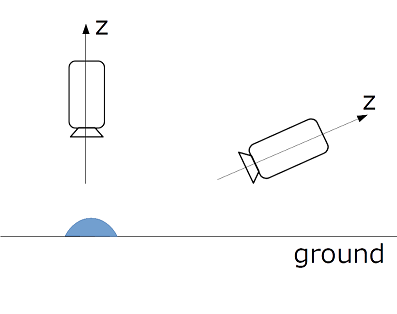
Fig7. Z軸の向き(z-axis direction)
Woodhamの手法について
照度差ステレオは1980年にWoodhamにより基本的な手法が提案されました[1]。
- 拡散反射、ランバート反射
物体に光が当たり反射する際、拡散反射(diffuse reflection)や鏡面反射が起こります。
鏡面反射は入射光は入射角と反射角が等しくなるよう物体表面で反射し、表面の輝度は正反射方向と視線が同じ向きの場合に最も明るくなります。
拡散反射では入射光が物体の表面層内部で吸収、散乱を繰り返し、散乱光は様々な方向から外部へ出てきます。均等拡散反射(uniform diffuse reflection)面では表面の輝度は視線によらず同じ明るさです。
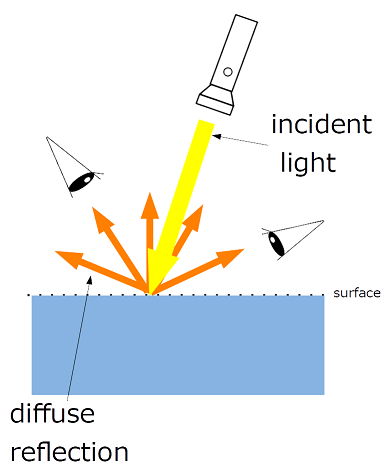
Fig8.均等拡散反射(uniform diffuse reflection)
![\[ d=(\bm{l} \cdot \bm{n}) ai \]](form_476.png)
ただし
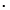 :ベクトルの内積、
:ベクトルの内積、
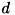 :物体表面の輝度、
:物体表面の輝度、
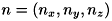 :単位法線ベクトル、
:単位法線ベクトル、
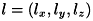 :単位光源ベクトル、
:単位光源ベクトル、
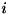 :入射光の輝度、
:入射光の輝度、
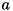 :拡散反射率(アルベド)
:拡散反射率(アルベド)
とします。
- 法線推定
- どの光源も平行光源で輝度は同一とし、環境光の影響は考えず、物体表面ではランバート反射だけが起きているとします。 法線は画素ごと独立にすべての画素で計算します。 以下では撮像した画像たちの画素の位置を固定して考えます。 光源の数を
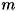 とし、光源方向を
とし、光源方向を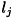 、
、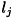 で撮像された物体表面の輝度を
で撮像された物体表面の輝度を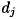 とおきます(
とおきます(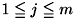 )。 このとき光源の数だけランバート反射の式が得られ、以下のように表されます。
)。 このとき光源の数だけランバート反射の式が得られ、以下のように表されます。 ![\[ \left\{ \begin{alignedat}{4} (l_{1,x}n_{x}+{} && l_{1,y}n_{y}+{} && l_{1,z}n_{z}) && ai={} && d_{1} \\ (l_{2,x}n_{x}+{} && l_{2,y}n_{y}+{} && l_{2,z}n_{z}) && ai={} && d_{2} \\ \vdots \\ (l_{m,x}n_{x}+{} && l_{m,y}n_{y}+{} && l_{m,z}n_{z}) && ai={} && d_{m} \\ \end{alignedat} \right. \]](form_487.png)
ここで
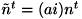 とおいて、
とおいて、 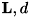 をそれぞれ
をそれぞれ ![\[ \textbf{L}= \begin{pmatrix} l_{1,x} & l_{1,y} & l_{1,z} \\ l_{2,x} & l_{2,y} & l_{2,z} \\ \vdots & \vdots & \vdots \\ l_{m,x} & l_{m,y} & l_{m,z} \end{pmatrix}, \bm{d}=\begin{pmatrix}d_{1} \\ d_{2} \\ \vdots \\ d_{m} \end{pmatrix} \]](form_490.png)
とおきます。式を書き換えると
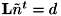 と書け、
と書け、 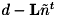 のノルムが最小となるような
のノルムが最小となるような 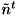 を最小二乗法によりもとめます。その後得られた
を最小二乗法によりもとめます。その後得られた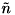 を正規化し単位法線ベクトル
を正規化し単位法線ベクトル 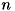 を得ます。 入射光輝度
を得ます。 入射光輝度 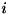 が既知の場合はアルベドも求めることが出来ます。
が既知の場合はアルベドも求めることが出来ます。
- アルベド
- 入射光は拡散反射や鏡面反射、吸収されるなど様々ですが、アルベドは入射光のうちどれくらいが拡散反射するかを表す定数で、ランバート反射に置ける式中の
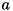 にあたります。アルベドは物体の色、明るさに関係します。 本ライブラリでは入射光輝度
にあたります。アルベドは物体の色、明るさに関係します。 本ライブラリでは入射光輝度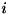 は画像型に応じた定数であるとした場合のアルベド画像を計算します。
は画像型に応じた定数であるとした場合のアルベド画像を計算します。
- 注意
- Woodhamによる照度差ステレオでは「物体表面はランバート反射だけであり、鏡面反射等を考えない」「光源は環境光を考えず平行光源だけ」という、厳しい仮定となっています。仮定を大幅に満たさない状況では、法線を推定がうまく出来ないことも有り得ます。 また撮像対象の物体について、物体同士で重なりがある場合やカメラ光軸と平行な物体の面面が存在する場合があり、本手法ではそのような箇所では撮像画像だけから法線を得ることは困難です。
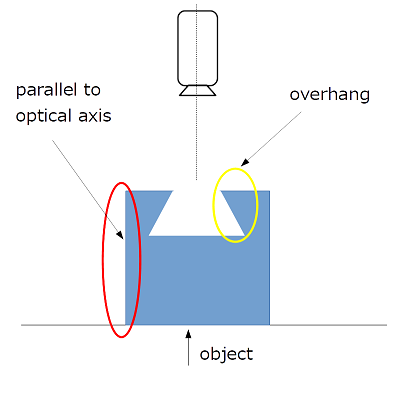
Fig9.物体の形状が原因で法線が求まらない例
高さ画像について
物体が写っている画像の座標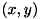 が決まると物体の表面の高さ
が決まると物体の表面の高さ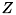 は決まると考え、
は決まると考え、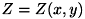 とします。 表面法線
とします。 表面法線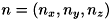 が得られたとき、そこから勾配
が得られたとき、そこから勾配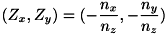 を求めることができます。 ここで
を求めることができます。 ここで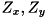 はそれぞれ高さ
はそれぞれ高さ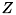 の
の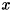 に関する偏微分、
に関する偏微分、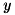 に関する偏微分とします。
に関する偏微分とします。相対的な高さについて勾配を線積分をすれば求まりますが、照度差ステレオで求めた法線は誤差が含まれることがあり、 そのまま積分した場合は高さの誤差が大きくなってしまうことがあります。
本ライブラリでは、高さの誤差を低減するよう工夫して計算する関数を二つ用意しています。
- 使用例
- サンプルコード
- 参考文献:
- [1]Rober J.Woodham(1980), "Photometric Method for Determining Surface Orientation from Multiple Images"
- [2]画像情報教育振興協会(2015), "ディジタル画像処理[改訂新版]", p.337,341,344,348~350