テクスチャ解析
[画像統計量]


関数
INT FVALGAPI	fnFIE_texture_first_order_statistics (FHANDLE hsrc, DOUBLE ave, DOUBLE sgm2, DOUBLE skewness, DOUBLE kurtosis)
	濃淡ヒストグラムの算出
INT FVALGAPI	fnFIE_texture_coocurrence_matrix (FHANDLE hsrc, INT dx, INT dy, INT gray_level, FMATRIX *mat)
	同時生起行列の算出
INT FVALGAPI	fnFIE_texture_calc_gcm_entropy (const FMATRIX mat, DOUBLE entropy)
	同時生起行列を用いたエントロピーの算出
INT FVALGAPI	fnFIE_texture_calc_gcm_energy (const FMATRIX mat, DOUBLE energy)
	同時生起行列を用いたエネルギーの算出
INT FVALGAPI	fnFIE_texture_calc_gcm_inertia (const FMATRIX mat, DOUBLE inertia)
	同時生起行列を用いた慣性の算出
INT FVALGAPI	fnFIE_texture_calc_gcm_local_homogeneity (const FMATRIX mat, DOUBLE lh)
	同時生起行列を用いた局所一様性の算出

関数

INT FVALGAPI fnFIE_texture_first_order_statistics	(	FHANDLE	hsrc,
		DOUBLE *	ave,
		DOUBLE *	sgm2,
		DOUBLE *	skewness,
		DOUBLE *	kurtosis
	)

濃淡ヒストグラムの算出

１次統計量である平均値（μ）、分散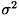（ $\sigma^{2}$ ）、そして特徴量の歪度(Skewness)、尖度(Kurtosis) を全体が１となるように正規化されたヒストグラムから算出します。テクスチャ解析では濃淡ヒストグラムと呼ばれる手法です。関数内部でのヒストグラムの作成には fnFIE_make_histogram() が利用されています。

歪度、尖度を求める式はそれぞれ

$Skewness = \left(\sum \left( i - \mu \right)^{3}H\left( i \right)\right) / \sigma^{3}$

$Kurtosis = \left(\sum \left( i - \mu \right)^{4}H\left( i \right)\right) / \sigma^{4}$

となります。ここで、歪度は、尖度は、それぞれ重心まわりの３次および４次モーメントとなります。なお、歪度、尖度の計算にはσによる除算が必要ですが、σが０の場合は、skewness と kurtosis には０が代入されます。

なお ave, sgm2, skewness, kurtosis のうち、取得する必要のない統計量がある場合は、そのパラメータに NULL を指定してください。ただし、これら４つのすべてに NULL が指定された場合は F_ERR_INVALID_PARAM エラーとなります。

引数:

`[in]`	hsrc	入力画像( type: uc8, us16 / ch : 1 )
`[out]`	ave	平均値(μ)
`[out]`	sgm2	分散( 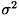$\sigma^{2}$ )
`[out]`	skewness	歪度(Skewness)
`[out]`	kurtosis	尖度(Kurtosis)

戻り値:

	F_ERR_NONE	正常終了
	F_ERR_INVALID_IMAGE	不正な画像オブジェクトが渡された
	F_ERR_INVALID_PARAM	不正なパラメータが渡された ave, sgm2, skewness, kurtosis, すべてがNULL
	F_ERR_NOMEMORY	メモリ不足
	F_ERR_NO_LICENCE	ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_texture_coocurrence_matrix	(	FHANDLE	hsrc,
		INT	dx,
		INT	dy,
		INT	gray_level,
		FMATRIX *	mat
	)

同時生起行列の算出

指定した領域の同時生起行列 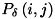$P_{\delta }\left(i,j\right)$ を求めます。同時生起行列とは、画像（領域）内の濃淡ｉのある基準点から ( dx , dy ) だけ離れた点の濃淡がｊである確率をｉｊ成分とする行列のことです。本関数では、上記確率に濃淡ｉの点から( -dx , -dy )だけ離れた点の濃淡がｊである確率を加えており、求められる行列は対称行列となります。なお、 | dx | と | dy | は、画像の幅と高さを width 、 height とした場合、以下の条件を満たしている必要があります。つまり、 ( dx , dy ) だけ離れた点が、画像内のどのような基準点にも存在しない場合は、エラーとなります。

| dx | < width
| dy | < height

画像の階調数をＮとすると同時生起行列はＮ×Ｎの正方行列となります（値は 0～N-1）。本関数では濃度階調数を gray_level によって自由に設定できますが、入力画像の各画素の濃度値は 0 ～ gray_level の範囲に収まっていなければいけません。さもなければ内部でメモリアクセス違反が発生します。ただし、指定する階調数と同時生起行列（ mat ）の mat->row および、 mat->col は同じ値である必要があり、FMATRIX が確保できるサイズに制限があるため、 gray_level には 16384 未満の値を指定しなければなりません。また、出力の mat は、あらかじめ呼び出し側で必要なサイズを確保しておいてください。

同時生起行列を求めるための、簡単な例を示します。画像が以下のように与えられたものとします。

$\left| \begin{array}{c|c|c|c} \hline 0 & 0 & 1 & 1 \\ \hline 0 & 0 & 1 & 1 \\ \hline 0 & 2 & 2 & 2 \\ \hline 2 & 2 & 3 & 3 \\ \hline \end{array} \right|$

この場合、階調数は４となり、同時生起行列は４×４となります。ここで、 dx=1 , dy=0 を考えます。注目画素が 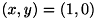$(x,y)=(1,0)$ では濃度値が０、 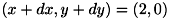$(x+dx,y +dy)=(2,0)$ の濃度値は１であるため、同時生起行列を 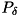$P_{\delta}$ とすると、 $P_{\delta}[0][1]$ と $P_{\delta}[1][0]$ にそれぞれ１を加えます。この処理を有効な画素に対して繰り返します。

参考のために、上記画像データに対して、 dx と dy を変化されたいくつかの同時生起行列を示します。なお、下記の例では各要素の値をわかり易くするために整数値で表していますが、本関数で取得される実際の行列の要素はすべて確率となっています。つまり、下記の例で示した行列の各値を要素の総数で割った値が実際の要素の値になります。

dx=1 , dy=0

$P1_{\delta } = \left[ \begin{array}{cccc} 4 & 2 & 1 & 0 \\ 2 & 4 & 0 & 0 \\ 1 & 0 & 6 & 1 \\ 0 & 0 & 1 & 2 \\ \end{array} \right]$

dx=0 , dy=1

$P2_{\delta } = \left[ \begin{array}{cccc} 6 & 0 & 2 & 0 \\ 0 & 4 & 2 & 0 \\ 2 & 2 & 2 & 2 \\ 0 & 0 & 2 & 0 \\ \end{array} \right]$

dx=1 , dy=1

$P3_{\delta } = \left[ \begin{array}{cccc} 2 & 1 & 3 & 0 \\ 1 & 2 & 1 & 0 \\ 3 & 1 & 0 & 2 \\ 0 & 0 & 2 & 0 \\ \end{array} \right]$

dx=-1 , dy=1

$P4_{\delta } = \left[ \begin{array}{cccc} 4 & 1 & 0 & 0 \\ 1 & 2 & 2 & 0 \\ 0 & 2 & 4 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right]$

引数:

`[in]`	hsrc	入力画像( type : uc8, us16 / ch : 1 ) 幅、および高さは２以上
`[in]`	dx	水平方向パラメータ
`[in]`	dy	垂直方向パラメータ
`[in]`	gray_level	入力画像の階調数（１以上）
`[out]`	mat	同時生起行列 mat->row == mat->col == gray_level 1 < mat->row < 16384 かつ 1 < mat->col < 16384

戻り値:

	F_ERR_NONE	正常終了
	F_ERR_INVALID_IMAGE	不正な画像が渡された
	F_ERR_INVALID_PARAM	不正なパラメータが渡された \| dx \| >= width または、 \| dy \| >= height gray_level が１未満不正な mat
	F_ERR_NO_LICENCE	ライセンスエラー、または未初期化エラー

参考文献:

新編画像解析ハンドブック, 高木幹雄下田陽久, 東京大学出版会 ISBN 4-13-061119-4, 5.4.1.2 (pp.1262)

INT FVALGAPI fnFIE_texture_calc_gcm_entropy	(	const FMATRIX *	mat,
		DOUBLE *	entropy
	)

同時生起行列を用いたエントロピーの算出

fnFIE_texture_coocurrence_matrix() にて求めた同時生起行列 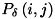$P_{\delta }\left(i,j\right)$ を用いてエントロピー( entropy )を計算します。

$entropy = - \sum_{i} \sum_{j} P_{\delta }\left(i,j\right)\log P_{\delta }\left(i,j\right)$

引数:

`[in]`	mat	同時生起行列 mat->row == mat->col 0 < mat->row < 16384 かつ 0 < mat->col < 16384 mat->row を入力画像の階調数とする
`[out]`	entropy	エントロピー

戻り値:

	F_ERR_NONE	正常終了
	F_ERR_INVALID_PARAM	不正なパラメータが渡された
	F_ERR_NO_LICENCE	ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_texture_calc_gcm_energy	(	const FMATRIX *	mat,
		DOUBLE *	energy
	)

同時生起行列を用いたエネルギーの算出

fnFIE_texture_coocurrence_matrix() にて求めた同時生起行列 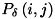$P_{\delta }\left(i,j\right)$ を用いてエネルギー( energy )を計算します。

$energy = \sum_{i} \sum_{j} \left\{P_{\delta }\left(i,j\right) \right\}^{2}$

引数:

`[in]`	mat	同時生起行列 mat->row == mat->col 0 < mat->row < 16384 かつ 0 < mat->col < 16384 mat->row を入力画像の階調数とする
`[out]`	energy	エネルギー

戻り値:

	F_ERR_NONE	正常終了
	F_ERR_INVALID_PARAM	不正なパラメータが渡された
	F_ERR_NO_LICENCE	ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_texture_calc_gcm_inertia	(	const FMATRIX *	mat,
		DOUBLE *	inertia
	)

同時生起行列を用いた慣性の算出

fnFIE_texture_coocurrence_matrix() にて求めた同時生起行列 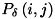$P_{\delta }\left(i,j\right)$ を用いて慣性( inertia )を計算します。

$inertia = \sum_{i} \sum_{j}\left(i-j\right)^{2}P_{\delta }\left(i,j\right)$

引数:

`[in]`	mat	同時生起行列 mat->row == mat->col 0 < mat->row < 16384 かつ 0 < mat->col < 16384 mat->row を入力画像の階調数とする
`[out]`	inertia	慣性

戻り値:

	F_ERR_NONE	正常終了
	F_ERR_INVALID_PARAM	不正なパラメータが渡された
	F_ERR_NO_LICENCE	ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_texture_calc_gcm_local_homogeneity	(	const FMATRIX *	mat,
		DOUBLE *	lh
	)

同時生起行列を用いた局所一様性の算出

fnFIE_texture_coocurrence_matrix() にて求めた同時生起行列 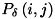$P_{\delta }\left(i,j\right)$ を用いて局所一様性( LH )を計算します。

$LH = \sum_{i} \sum_{j} \frac{P_{\delta }\left(i,j\right)}{1+\left(i-j\right)^{2}}$

引数:

`[in]`	mat	同時生起行列 mat->row == mat->col 0 < mat->row < 16384 かつ 0 < mat->col < 16384 mat->row を入力画像の階調数とする
`[out]`	lh	局所一様性

戻り値:

	F_ERR_NONE	正常終了
	F_ERR_INVALID_PARAM	不正なパラメータが渡された
	F_ERR_NO_LICENCE	ライセンスエラー、または未初期化エラー

テクスチャ解析 [画像統計量]

関数

関数

テクスチャ解析
[画像統計量]