凸包
[幾何計算]
説明
2次元凸包を作成するライブラリです。堅苦しい定義を記すと「点集合の凸包とは、その点集合を含む最小の凸多角形」です。 直感的には、木の板に釘を(同じ面に)いくつか打ち付けた後、その釘がすべて入るように外側から輪 ゴムで留めたときにできる輪ゴムの形が(釘の集合の)凸包となります。 データ解析的には凸多角形という非常に扱い易い形で点集合全体を近似している、と考えられます。
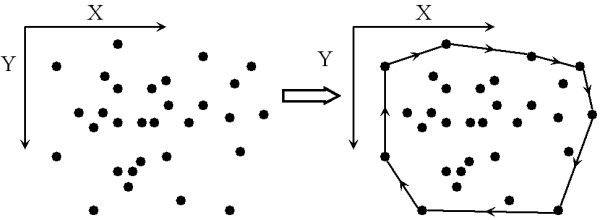
処理速度のオーダーは O( n log n ) です。 (凸包生成ルーチンのオーダーは O(n) ですが、前処理のソートのオーダーが支配的であるため。)
- 参考文献:
- D.Avis 他 入門 有限・離散の数学4「計算幾何学・離散幾何学」第2章、(朝倉書店) 1994
関数 | |
| INT FVALGAPI | fnFIE_convex2d_monochain (const DPNT_T *pnts, INT iPntsNum, DPNT_T **ppHull, INT *ipVerNum) |
| Monotone Chain法による二次凸包作成 | |
関数
| INT FVALGAPI fnFIE_convex2d_monochain | ( | const DPNT_T * | pnts, | |
| INT | iPntsNum, | |||
| DPNT_T ** | ppHull, | |||
| INT * | ipVerNum | |||
| ) |
Monotone Chain法による二次凸包作成
Monotone Chain法によって、入力された2次元点データの凸包を作成します。 出力される凸包の頂点列はデカルト座標系の上で時計回りとなります。(図参照)

最初と最後の頂点は同じ点であるため、出力される凸包の頂点数は実の頂点数プラス1になります。 凸包保存用メモリは関数内部に確保するため、パラメタを渡すときに *ppHull は必ずNULLにしなければなりません。 入力点数は3点以上なければいけません。
凸包を構成する前に内部点の除去を行なうことにより、平均的に処理時間を短縮しています。
与えられる入力点はソートしなくても、重複点があっても構いません。 入力点列が一直線上にある場合や、すべて同一点だった場合などの時には F_ERR_CALC_IMPOSSIBLE を返します。
機械計算誤差があるため、入力点の距離が小さ過ぎる場合に、あるいは点の座標が大き過ぎる場合に 正しい凸包にならない可能性があります。
作成された凸包の頂点列 *ppHull は不要になったら fnOAL_free() にて解放してください。
- 注意:
- 以下の関数で利用する場合は、頂点の個数( ipVerNum )から1引いた個数( ipVerNum - 1 )を指定してください。 本関数では、最初と最後の頂点が同じ点となるため、出力された出力される凸包の頂点列をそのまま利用すると凸包と判定されません。
- fnFIE_cg_convex_polygon_check()
- fnFIE_cg_convex_polygon_check_d()
- fnFIE_cg_simple_polygon_check()
- fnFIE_cg_simple_polygon_check_d()
- fnFIE_cg_polygon_area_calc()
- fnFIE_cg_polygon_area_calc_d()
- fnFIE_cg_convex_polygon_diameter()
- fnFIE_cg_convex_polygon_diameter_d()
- fnFIE_cg_pos_point_to_convex_polygon()
- fnFIE_cg_pos_point_to_simple_polygon()
- fnFIE_cg_points_in_convex_polygon()
- fnFIE_cg_points_in_simple_polygon()
- 引数:
-
[in] pnts 入力点集合配列 [in] iPntsNum 入力点の数(3点以上) [out] ppHull 出力される凸包の頂点列( *ppHull は必ずNULLでなければならない) [out] ipVerNum 出力される凸包の頂点の個数
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_NOMEMORY メモリ不足で確保に失敗した F_ERR_INVALID_PARAM パラメータ不正 F_ERR_CALC_IMPOSSIBLE 入力点列が一直線上にある、或いはすべて同一点だった F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 使用例:
// エラー処理は省略しているので注意して下さい。 #include "fie.h" #include "oal_aloc.h" //メモリ管理 //出力画像の幅と高さ及び,入力点数 #define WIDTH 206 #define HEIGHT 204 #define PNTS_NUM 20 VOID convex2d_monochain() { //変数宣言部 INT i; //ループ変数 //二次凸包計算用変数 DPNT_T dpnts[PNTS_NUM]; //入力点集合配列 INT pnts_num = PNTS_NUM; //入力点の数(3点以上) DPNT_T * phull = NULL; //出力される凸包の頂点列( *phull は必ずNULLでなければならない) INT ver_num; //出力される凸包の頂点の個数 //描画用変数 DOUBLE val=0; //描画用矩形,線分,凸包の濃度値 FHANDLE hdst = NULL; //結果画像 //チャイルド画像 FHANDLE hrgb_r = NULL; FHANDLE hrgb_g = NULL; FHANDLE hrgb_b = NULL; //処理部 //出力画像の領域を確保します hdst = fnFIE_img_root_alloc( F_IMG_UC8, 3, WIDTH, HEIGHT ); //チャイルド画像の領域を確保 hrgb_r = fnFIE_img_child_alloc_single_ch(hdst, 0, 0, 0, WIDTH, HEIGHT); hrgb_g = fnFIE_img_child_alloc_single_ch(hdst, 1, 0, 0, WIDTH, HEIGHT); hrgb_b = fnFIE_img_child_alloc_single_ch(hdst, 2, 0, 0, WIDTH, HEIGHT); //出力画像を白色(255)で塗りつぶす fnFIE_img_clear(hdst, 255); //入力点群 dpnts[0].x=50,dpnts[0].y=60; dpnts[1].x=15,dpnts[1].y=96; dpnts[2].x=35,dpnts[2].y=52; dpnts[3].x=22,dpnts[3].y=106; dpnts[4].x=55,dpnts[4].y=116; dpnts[5].x=65,dpnts[5].y=126; dpnts[6].x=101,dpnts[6].y=168; dpnts[7].x=19,dpnts[7].y=65; dpnts[8].x=66,dpnts[8].y=55; dpnts[9].x=182,dpnts[9].y=98; dpnts[10].x=152,dpnts[10].y=78; dpnts[11].x=36,dpnts[11].y=124; dpnts[12].x=45,dpnts[12].y=156; dpnts[13].x=150,dpnts[13].y=180; dpnts[14].x=147,dpnts[14].y=100; dpnts[15].x=170,dpnts[15].y=170; dpnts[16].x=132,dpnts[16].y=78; dpnts[17].x=111,dpnts[17].y=50; dpnts[18].x=122,dpnts[18].y=13; dpnts[19].x=44,dpnts[19].y=84; //入力点の描画 for(i=0; i<pnts_num; i++) { //入力点を半径2の円で描画する fnFIE_draw_circle(hrgb_r, &val, F_DRAW_FILL_IN, dpnts[i], 2); fnFIE_draw_circle(hrgb_g, &val, F_DRAW_FILL_IN, dpnts[i], 2); fnFIE_draw_circle(hrgb_b, &val, F_DRAW_FILL_IN, dpnts[i], 2); } //二次凸包の計算 fnFIE_convex2d_monochain(dpnts, pnts_num, &phull, &ver_num); //二次凸包の描画 fnFIE_draw_polygon(hrgb_g, &val, F_DRAW_LINE, phull, (ver_num-1)); fnFIE_draw_polygon(hrgb_b, &val, F_DRAW_LINE, phull, (ver_num-1)); //結果画像を保存します fnFIE_save_png("result.png", hdst, -1); //解放 fnOAL_free(phull); //取得した凸包の頂点列の開放 fnFIE_free_object( hdst ); //結果画像領域の解放 fnFIE_free_object( hrgb_r ); //チャイルド画像領域の解放 fnFIE_free_object( hrgb_g ); //チャイルド画像領域の解放 fnFIE_free_object( hrgb_b ); //チャイルド画像領域の解放 } INT main(VOID) { // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); convex2d_monochain(); // 終了処理 fnFIE_teardown(); return 0; }
- 処理結果例:
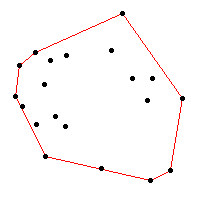
処理結果画像