多角形
[幾何計算]

説明

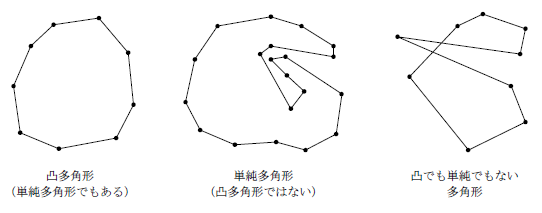
単純多角形、凸多角形とは
連続しないどの２辺も交差・接触しない多角形を単純多角形と言います(下図を参照)。 すなわち、その内部が１つの領域になっている多角形のことです。 一方、どの頂点も「へこんでいない」多角形を凸多角形と言います(下図を参照)。 厳密な定義は次の通り；「多角形の周囲および内部のどの２点を選んで線分で結んでも決してそ の線分が多角形の外部を通ることがないとき、この多角形は凸多角形である」となります。

fie_cg_std_polygon.png


列挙型

enum  f_cg_pnt_pos {
  F_CG_INNER_PNT = 1, F_CG_NOT_INNER_PNT = 2,
  F_CG_OUTER_PNT = 3, F_CG_BOUNDARY_PNT = 4
}
 点の位置 [詳細]

関数

INT FVALGAPI fnFIE_cg_convex_polygon_check (const PNT_T *vrtx, INT num, INT *convex_type)
 多角形の凸性のチェック(整数型)
INT FVALGAPI fnFIE_cg_convex_polygon_check_d (const DPNT_T *vrtx, INT num, INT *convex_type)
 多角形の凸性のチェック(浮動小数点型)
INT FVALGAPI fnFIE_cg_simple_polygon_check (const PNT_T *vrtx, INT num, INT *simple_type)
 多角形の単純性のチェック(整数型)
INT FVALGAPI fnFIE_cg_simple_polygon_check_d (const DPNT_T *vrtx, INT num, INT *simple_type)
 多角形の単純性のチェック(浮動小数点型)
INT FVALGAPI fnFIE_cg_polygon_area_calc (const PNT_T *vrtx, INT num, INT *area2)
 単純多角形の符号付面積(整数型)
INT FVALGAPI fnFIE_cg_polygon_area_calc_d (const DPNT_T *vrtx, INT num, DOUBLE *area)
 単純多角形の符号付面積(浮動小数点型)
INT FVALGAPI fnFIE_cg_convex_polygon_diameter (const PNT_T *vrtx, INT num, INT *ans_pnt1, INT *ans_pnt2, INT *diameter)
 凸多角形に関する最遠点対問題(整数型)
INT FVALGAPI fnFIE_cg_convex_polygon_diameter_d (const DPNT_T *vrtx, INT num, INT *ans_pnt1, INT *ans_pnt2, DOUBLE *diameter)
 凸多角形に関する最遠点対問題(浮動小数点型)
INT FVALGAPI fnFIE_cg_pos_point_to_convex_polygon (PNT_T pnt, const PNT_T *vrtx, INT num, enum f_cg_pnt_pos *pos)
 点の凸多角形に対する位置判定
INT FVALGAPI fnFIE_cg_pos_point_to_simple_polygon (PNT_T pnt, const PNT_T *vrtx, INT num, enum f_cg_pnt_pos *pos)
 点の単純多角形に対する位置判定
INT FVALGAPI fnFIE_cg_points_in_convex_polygon (const PNT_T *vrtx, INT vrtx_num, const PNT_T *pnts, INT pnt_num, INT bndry_flag, INT **ans_pnt_no, INT *ans_pnt_num)
 凸多角形内部点列挙の実行
INT FVALGAPI fnFIE_cg_points_in_simple_polygon (const PNT_T *vrtx, INT vrtx_num, const PNT_T *pnts, INT pnt_num, INT bndry_flag, INT **ans_pnt_no, INT *ans_pnt_num)
 単純多角形内部点列挙の実行

列挙型

enum f_cg_pnt_pos

点の位置

点の位置を表します。

列挙型の値:
F_CG_INNER_PNT  点が多角形の内部にある(境界上は含まない)
F_CG_NOT_INNER_PNT  点が多角形の内部にない
F_CG_OUTER_PNT  点が多角形の外部にある(境界上は含まない)
F_CG_BOUNDARY_PNT  点が多角形の辺(境界)上にある

関数

INT FVALGAPI fnFIE_cg_convex_polygon_check ( const PNT_T *  vrtx,
INT  num,
INT *  convex_type 
)

多角形の凸性のチェック(整数型)

与えられた多角形が凸多角形であるかどうかを三角形の符号付面積を用いて判定します。 頂点はどちら周りで与えられていても構いません。 頂点数 num には３以上の値としてください。

入力する多角形の頂点は整数型となります。 入力する多角形の頂点が浮動小数点型の場合は、 fnFIE_cg_convex_polygon_check_d() を使用してください。

引数:
[in] vrtx 多角形の頂点
[in] num 頂点数( vrtx の要素数)
[out] convex_type 多角形の凸形状
  • 0 多角形は凸ではない
  • 1 多角形は凸である
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
  • 頂点数が３未満
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_convex_polygon_check_d() , fnFIE_convex2d_monochain()

INT FVALGAPI fnFIE_cg_convex_polygon_check_d ( const DPNT_T *  vrtx,
INT  num,
INT *  convex_type 
)

多角形の凸性のチェック(浮動小数点型)

与えられた多角形が凸多角形であるかどうかを三角形の符号付面積を用いて判定します。 頂点はどちら周りで与えられていても構いません。 頂点数 num は３以上の値としてください。

入力する多角形の頂点は浮動小数点型となります。 入力する多角形の頂点が整数型の場合は、 fnFIE_cg_convex_polygon_check() を使用してください。

引数:
[in] vrtx 多角形の頂点
[in] num 頂点数( vrtx の要素数)
[out] convex_type 多角形の凸形状
  • 0 多角形は凸ではない
  • 1 多角形は凸である
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
  • 頂点数が３未満
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_convex_polygon_check() , fnFIE_convex2d_monochain()

INT FVALGAPI fnFIE_cg_simple_polygon_check ( const PNT_T *  vrtx,
INT  num,
INT *  simple_type 
)

多角形の単純性のチェック(整数型)

与えられた多角形が単純多角形であるかどうかを線分の交差判定を用いて判定します。 頂点はどちら周りで与えられていても構いません。

入力する多角形の頂点は整数型となります。 入力する多角形の頂点が浮動小数点型の場合は、 fnFIE_cg_simple_polygon_check_d() を使用してください。

頂点数 num は３以上の値としてください。

引数:
[in] vrtx 多角形の頂点
[in] num 頂点数( vrtx の要素数)
[out] simple_type 多角形の凸形状
  • 0 多角形は単純ではない
  • 1 多角形は単純である
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
  • 頂点数が３未満
F_ERR_NOMEMORY メモリ不足
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_simple_polygon_check_d()

INT FVALGAPI fnFIE_cg_simple_polygon_check_d ( const DPNT_T *  vrtx,
INT  num,
INT *  simple_type 
)

多角形の単純性のチェック(浮動小数点型)

与えられた多角形が単純多角形であるかどうかを線分の交差判定を用いて判定します。 頂点はどちら周りで与えられていても構いません。

入力する多角形の頂点は浮動小数点型となります。 入力する多角形の頂点が整数型の場合は、 fnFIE_cg_simple_polygon_check() を使用してください。

頂点数 num は３以上の値としてください。

引数:
[in] vrtx 多角形の頂点
[in] num 頂点数( vrtx の要素数)
[out] simple_type 多角形の凸形状
  • 0 多角形は単純ではない
  • 1 多角形は単純である
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
  • 頂点数が３未満
F_ERR_NOMEMORY メモリ不足
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_simple_polygon_check() , fnFIE_convex2d_monochain()

INT FVALGAPI fnFIE_cg_polygon_area_calc ( const PNT_T *  vrtx,
INT  num,
INT *  area2 
)

単純多角形の符号付面積(整数型)

与えられた単純多角形(座標は整数)の符号付面積を求めます。 面積の符号は多角形の頂点列が

  • 反時計周りの場合 → 正
  • 時計周りの場合 → 負
となるように決められています。 ただし、時計回りが正となる座標系で考えています。

入力する多角形の頂点は整数型となります。 入力する多角形の頂点が浮動小数点型の場合は、 fnFIE_cg_polygon_area_calc_d() を使用してください。

面積は２倍値であるので注意してください(公式から精度が 0.5 単位であることが保証されている)。

頂点数 num は３以上の値としてください。

引数:
[in] vrtx 多角形の頂点
[in] num 頂点数( vrtx の要素数)
[out] area2 単純多角形の符号付き面積の２倍値を返す
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
F_ERR_NOMEMORY メモリ不足
F_ERR_CALC_IMPOSSIBLE 頂点列が単純多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_polygon_area_calc_d()

INT FVALGAPI fnFIE_cg_polygon_area_calc_d ( const DPNT_T *  vrtx,
INT  num,
DOUBLE *  area 
)

単純多角形の符号付面積(浮動小数点型)

与えられた単純多角形の符号付面積を求めます。 面積の符号は多角形の頂点列が

  • 反時計周りの場合 → 正
  • 時計周りの場合 → 負
となるように決められています。 ただし、時計回りが正となる座標系で考えています。

入力する多角形の頂点は浮動小数点型となります。 入力する多角形の頂点が整数型の場合は、 fnFIE_cg_polygon_area_calc() を使用してください。

頂点数 num は３以上の値としてください。

引数:
[in] vrtx 多角形の頂点
[in] num 頂点数( vrtx の要素数)
[out] area 単純多角形の符号付き面積を返す
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
F_ERR_NOMEMORY メモリ不足
F_ERR_CALC_IMPOSSIBLE 頂点列が単純多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_polygon_area_calc() , fnFIE_convex2d_monochain()

INT FVALGAPI fnFIE_cg_convex_polygon_diameter ( const PNT_T *  vrtx,
INT  num,
INT *  ans_pnt1,
INT *  ans_pnt2,
INT *  diameter 
)

凸多角形に関する最遠点対問題(整数型)

与えられた凸多角形の頂点列で、最も離れている２点の番号とその距離の２乗を計算します。 アルゴリズムは「キャリパー法」と呼ばれるものです。

入力される凸多角形の頂点列の並びは時計回りあるいは反時計回りのいずれでも構いません。 任意の点集合の最遠点対問題は凸包を求めた後、このライブラリを使用することで、効率よく求めることができます。 ただし、すべての点が円周上にある場合などの特殊な場合や、 点の数がさほど多くない場合には単純な方法で処理する方が高速となります。

最遠点の２点は、 vrtx[ *ans_pnt1 ] と vrtx[ *ans_pnt2 ] となります。

なお、頂点数 num は１以上の値としてください。
もし、num = 1 であれば、*ans_pnt1 = *ans_pnt2 = 0 すなわち入力点が回答点となり、*diameter = 0 となります。
また、num = 2 でこれらが同一点の場合は、*ans_pnt1 = *ans_pnt2 = 0 および *diameter = 0 となります。
さらに、num >= 3 のときに頂点列のなかに同一点が含まれている場合、この頂点列は凸多角形ではないとして F_ERR_CALC_IMPOSSIBLE を返します。

入力する多角形の頂点は整数型となります。 入力する多角形の頂点が浮動小数点型の場合は、 fnFIE_cg_convex_polygon_diameter_d() を使用してください。

参考文献:
キャリパー法については、例えば以下を参照してください。
  • 浅野哲夫 著「計算幾何学」§3.2 (朝倉書店) 1990

引数:
[in] vrtx 凸多角形の頂点列
[in] num 頂点数
[out] ans_pnt1 回答点の番号１( vrtx の配列番号)
[out] ans_pnt2 回答点の番号２( vrtx の配列番号)
[out] diameter 最も離れている２点の距離(集合の直径)の２乗
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータを渡した
F_ERR_CALC_IMPOSSIBLE 頂点列が凸多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_cg_convex_polygon_diameter_d ( const DPNT_T *  vrtx,
INT  num,
INT *  ans_pnt1,
INT *  ans_pnt2,
DOUBLE *  diameter 
)

凸多角形に関する最遠点対問題(浮動小数点型)

与えられた凸多角形の頂点列で、最も離れている２点の番号とその距離の２乗を計算します。 アルゴリズムは「キャリパー法」と呼ばれるものです。

入力される凸多角形の頂点列の並びは時計回りあるいは反時計回りのいずれでも構いません。 任意の点集合の最遠点対問題は凸包を求めた後、このライブラリを使用することで、効率よく求めることができます。 ただし、すべての点が円周上にある場合などの特殊な場合や、 点の数がさほど多くない場合には単純な方法で処理する方が高速となります。

最遠点の２点は、 vrtx[ *ans_pnt1 ] と vrtx[ *ans_pnt2 ] となります。

なお、頂点数 num は１以上の値としてください。
もし、num = 1 であれば、*ans_pnt1 = *ans_pnt2 = 0 すなわち入力点が回答点となり、*diameter = 0 となります。
また、num = 2 でこれらが同一点の場合は、*ans_pnt1 = *ans_pnt2 = 0 および *diameter = 0 となります。
さらに、num >= 3 のときに頂点列のなかに同一点が含まれている場合、この頂点列は凸多角形ではないとして F_ERR_CALC_IMPOSSIBLE を返します。

入力する多角形の頂点は浮動小数点型となります。 入力する多角形の頂点が整数型の場合は、 fnFIE_cg_convex_polygon_diameter() を使用してください。

参考文献:
キャリパー法については、例えば以下を参照してください。
  • 浅野哲夫 著「計算幾何学」§3.2 (朝倉書店) 1990

引数:
[in] vrtx 凸多角形の頂点列
[in] num 頂点数
[out] ans_pnt1 回答点の番号１( vrtx の配列番号)
[out] ans_pnt2 回答点の番号２( vrtx の配列番号)
[out] diameter 最も離れている２点の距離(集合の直径)の２乗
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータを渡した
F_ERR_CALC_IMPOSSIBLE 頂点列が凸多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_cg_pos_point_to_convex_polygon ( PNT_T  pnt,
const PNT_T *  vrtx,
INT  num,
enum f_cg_pnt_pos *  pos 
)

点の凸多角形に対する位置判定

点が凸多角形に対してどの位置にあるかを、三角形の符号付面積を用いることにより求めます。 頂点はどちら周りで与えられていても構いません。 なお、頂点数 num は３以上の値としてください。

引数:
[in] pnt 位置判定したい点
[in] vrtx 凸多角形の頂点列
[in] num 多角形の頂点数( vetx の要素数)
[out] pos 凸多角形に対する点の位置
  • F_CG_INNER_PNT 点が多角形の内部にある(境界上は含まない)
  • F_CG_OUTER_PNT 点が多角形の外部にある(境界上は含まない)
  • F_CG_BOUNDARY_PNT 点が多角形の辺(境界)上にある
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された(頂点数が３未満)
F_ERR_NOMEMORY メモリ不足
F_ERR_CALC_IMPOSSIBLE 頂点列が凸多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_cg_pos_point_to_simple_polygon ( PNT_T  pnt,
const PNT_T *  vrtx,
INT  num,
enum f_cg_pnt_pos *  pos 
)

点の単純多角形に対する位置判定

点が単純多角形に対してどの位置にあるかを、その点を終点とする水平線分と辺の交差判定 を用いることにより求めます。 頂点はどちら周りで与えられていても構いません。 なお、頂点数 num は３以上の値としてください。

引数:
[in] pnt 位置判定したい点
[in] vrtx 単純多角形の頂点列
[in] num 多角形の頂点数( vetx の要素数)
[out] pos 凸多角形に対する点の位置
  • F_CG_INNER_PNT 点が多角形の内部にある(境界上は含まない)
  • F_CG_OUTER_PNT 点が多角形の外部にある(境界上は含まない)
  • F_CG_BOUNDARY_PNT 点が多角形の辺(境界)上にある
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された(頂点数が３未満)
F_ERR_NOMEMORY メモリ不足
F_ERR_CALC_IMPOSSIBLE 計算不能
  • 頂点列が単純多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー

INT FVALGAPI fnFIE_cg_points_in_convex_polygon ( const PNT_T *  vrtx,
INT  vrtx_num,
const PNT_T *  pnts,
INT  pnt_num,
INT  bndry_flag,
INT **  ans_pnt_no,
INT *  ans_pnt_num 
)

凸多角形内部点列挙の実行

点集合に対し、凸多角形の内部に含まれるものを列挙します。 多角形に対して前処理を行なうことによって、 fnFIE_cg_pos_point_to_convex_polygon() を繰返しを用いるよりも高速に処理出来ることを想定しています。 具体的には、点の含まれる可能性のある各領域を二分探索法によって求める、というものです。

回答としては内部にある点の番号表を与えます。 境界(多角形の辺)上にある点を回答に含めるかどうかの選択が可能です。

なお各パラメータは、以下の条件を満たす必要があります。

  • 多角形の頂点数( vrtx_num )は３以上、内部判定する点数( pnt_num )は１以上の値を入力してください。
  • ans_pnt_no は、関数内部で必要なメモリを確保します。 メモリを確保した配列を指定しないでください。 また、 *ans_pnt_no がNULLで初期化されていない場合は、エラーとなります。 確保されたメモリは、 fnOAL_free() で解放してください。
  • bndry_flag は ON または OFF 以外を指定した場合、 F_ERR_INVALID_PARAM が返されます。
参考文献:
  • 「プレパラータ・シェーモス「計算幾何学」§２．２」
引数:
[in] vrtx 凸多角形の頂点列
[in] vrtx_num 多角形の頂点数( vrtx の要素数)
[in] pnts 内部点を判定する点集合 このデータは順序データで有る必要はなく、また重複点が合ってもかまわない
[in] pnt_num 点集合の点の数( pnts の要素数)
[in] bndry_flag 境界フラグ
  • ON 境界上の点を内部の点として回答に含める
  • OFF 境界上の点は外部の点として、回答に含めない
[out] ans_pnt_no 内部にある点の番号列の先頭ポインタ。 ここでの番号とは、配列 pnts での要素番号を指す
[out] ans_pnt_num 内部点の数
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
F_ERR_NOMEMORY メモリ不足
F_ERR_CALC_IMPOSSIBLE 計算不能
  • 頂点列が凸多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_pos_point_to_convex_polygon()

INT FVALGAPI fnFIE_cg_points_in_simple_polygon ( const PNT_T *  vrtx,
INT  vrtx_num,
const PNT_T *  pnts,
INT  pnt_num,
INT  bndry_flag,
INT **  ans_pnt_no,
INT *  ans_pnt_num 
)

単純多角形内部点列挙の実行

点集合に対し、単純多角形の内部に含まれるものを列挙します。 多角形に対して前処理を行なうことによって、 fnFIE_cg_pos_point_to_simple_polygon() を繰返し用いるよりも高速に処理出来ることを想定しています。 具体的には、多角形の存在領域を分割して交差を調べる辺の数を減らす、というものです。

回答としては内部にある点の番号表を与えます。 境界(多角形の辺)上にある点を回答に含めるかどうかの選択が可能です。

なお各パラメータは、以下の条件を満たす必要があります。

  • 多角形の頂点数( vrtx_num )は３以上、内部判定する点数( pnt_num )は１以上の値を入力してください。
  • ans_pnt_no は、関数内部で必要なメモリを確保します。 メモリを確保した配列を指定しないでください。 また、 *ans_pnt_no がNULLで初期化されていない場合は、エラーとなります。 確保されたメモリは、 fnOAL_free() で解放てください。
  • bndry_flag は ON または OFF 以外を指定した場合、 F_ERR_INVALID_PARAM が返されます。
引数:
[in] vrtx 凸多角形の頂点列
[in] vrtx_num 多角形の頂点数( vrtx の要素数)
[in] pnts 内部点を判定する点集合 このデータは順序データで有る必要はなく、また重複点が合ってもかまわない
[in] pnt_num 点集合の点の数( pnts の要素数)
[in] bndry_flag 境界フラグ
  • ON 境界上の点も内部点と見なす
  • OFF 境界上の点は内部点とは見なさない
[out] ans_pnt_no 内部にある点の番号列の先頭ポインタ。 ここでの番号とは、配列 pnts での要素番号を指す
[out] ans_pnt_num 内部点の数
戻り値:
F_ERR_NONE 正常終了
F_ERR_INVALID_PARAM 不正なパラメータが渡された
F_ERR_NOMEMORY メモリ不足
F_ERR_CALC_IMPOSSIBLE 頂点列が単純多角形ではないため、計算不能（頂点数が３以上の場合）
F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
参照:
fnFIE_cg_pos_point_to_simple_polygon()

Documentation copyright © 2009-2024 FAST Corporation.
Generated on Fri Aug 9 16:38:47 2024 for FIEライブラリ by doxygen 1.5.6-FASTSP-p2