近似計算
[幾何計算]
説明
最小二乗法とロバスト推定法
通常、与えられたデータには誤差が含まれています。 測定値の中で想定される誤差範囲内にあるものをインライア、明らかに誤りであるものをアウトライア、外れ値と呼びます。 外れ値が存在することで、測定結果からのフィッティングに影響がでるため、外れ値を排除する必要があります。 ロバスト推定法は、外れ値をある程度含むようなデータからでも、比較的安定したモデルのパラメータを推定することができます。最小二乗法
二乗誤差を最小にするのが最小二乗法です。 最小二乗法は、外れ値に対してロバストではありません。 LMS 基準は以下のようになります。
![\[ {\rm LMS} = \min\ \sum _{i} \epsilon _{i} ^{2} \]](form_1001.png)
なお、 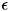 は誤差を表します。
は誤差を表します。
ロバスト推定法(M推定法)
二乗誤差基準では、誤差が大きいほど値が大きくなます。 ある一定以上の誤差で値の上昇を抑えることで、外れ値の影響を小さくする手法がM推定法です。 つまり、外れ値には小さいな重みを与えるように変形し、評価基準とします。 最小二乗法基準はすべての誤差に均等な重みで扱っているために、ひとつの大きな外れ値によって大きな影響を受けてしまいます。 評価基準は以下のようになります。
![\[ {\rm M} = \min\ \sum _{i} \rho \left( \epsilon _{i} \right) \]](form_1003.png)
なお、 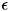 は誤差、
は誤差、 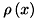 は重みを与えるための関数です。
は重みを与えるための関数です。
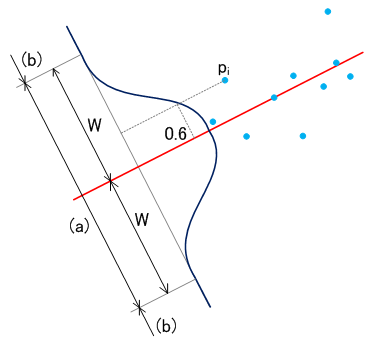
参考のために、M推定法による直線近似の例を下図に示します。 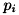 は計算対象となる点、 W は重みです。 この例での重みは 0.6 となります。 そして、 (a) は、直線を算出する際に、重みを加味して計算する領域、(b) は、直線を算出する際に、全く使われないデータとする領域となります。
は計算対象となる点、 W は重みです。 この例での重みは 0.6 となります。 そして、 (a) は、直線を算出する際に、重みを加味して計算する領域、(b) は、直線を算出する際に、全く使われないデータとする領域となります。
ロバスト推定法(ランザック法)
与えられた点群から、ランダムにいくつかのサンプル点を抽出して、最小二乗法に当てはめることを繰り返します。 抽出したサンプル点に外れ値が含まれていなければ、より確からしい推定を得ることができます。 かつ、外れ値が全点群の個数と比較して少なければ、推定される誤差範囲内に、より多くの点が含まれることになります。 このことから、最も多くの点が範囲内に含まれた場合の推定値を、正しい推定とする手法が、ランザック法です。ロバスト推定法(最小メディアン法)
与えられた点群から、ランダムにいくつかのサンプル点を抽出して、最小二乗法に当てはめることを繰り返します。 ランザック法との違いは、この場合の評価方法です。 最小メディアン法では、全測定値における二乗誤差の中央値が最も小さい場合の推定値を、正しい推定とします。 LMedS 基準は以下のようになります。
![\[ {\rm LMedS} = \min\left( med\ \epsilon _{i} ^2 \right) \]](form_1006.png)
なお、 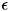 は誤差、 med は中央値を取ることを表します。
は誤差、 med は中央値を取ることを表します。
各手法の比較
- ロバスト性:最小メディアン法、ランザック法、M推定法、最小二乗法の順でロバストです。
- 実行時間:最小二乗法、M推定法、ランザック法、最小メディアン法の順で高速です。
- 最小メディアン法は誤差範囲が不明な場合に、ランザック法は明らかな場合に有効です。
列挙型 | |
| enum | f_pfit_calc_mode { F_PFIT_LSQ, F_PFIT_LSQ_SCALE, F_PFIT_RBST, F_PFIT_RBST_SCALE, F_PFIT_MINMAX, F_PFIT_MINMAX_SCALE } |
| 点群マッチングの処理選択 [詳細] | |
| enum | f_fit_mode { F_FIT_LSM = 0, F_FIT_MESTIMATOR = 1, F_FIT_RANSAC = 2, F_FIT_LMEDS = 3, F_FIT_LSM_FAST = 4, F_FIT_MESTIMATOR2 = 101, F_FIT_LMEDS2 = 103 } |
| 最小二乗法・ロバスト推定の処理選択 [詳細] | |
関数 | |
| INT FVALGAPI | fnFIE_pfit_coord (INT iPntNum, DPNT_T taOldPnt[], DPNT_T taNewPnt[], DOUBLE dSigmaCoef, enum f_pfit_calc_mode iCalcMode, DOUBLE *dpXc, DOUBLE *dpYc, DOUBLE *dpTheta, DOUBLE *dpScale) |
| 点群マッチングによる座標系パラメータ(原点座標,傾きおよびスケール)の算出 | |
| INT FVALGAPI | fnFIE_pfit_points (INT iPntNum, DPNT_T taWork[], DPNT_T taMaster[], DOUBLE dSigmaCoef, enum f_pfit_calc_mode iCalcMode, DPNT_T taConv[], DOUBLE daErr[]) |
| 点群マッチング後の座標値および誤差の算出 | |
| INT FVALGAPI | fnFIE_pfit_param (INT iPntNum, DPNT_T taWork[], DPNT_T taMaster[], DOUBLE dSigmaCoef, enum f_pfit_calc_mode iCalcMode, DOUBLE *dpXcOrg, DOUBLE *dpYcOrg, DOUBLE *dpXc, DOUBLE *dpYc, DOUBLE *dpTheta, DOUBLE *dpScale) |
| 点群マッチングの変換パラメータ(重心,回転角およびスケール)算出 | |
| INT FVALGAPI | fnFIE_cg_vectorize2d_cone (const PNT_T *src, UINT num_src, PNT_T *dst, UINT *index, UINT *num_dst, DOUBLE radius) |
| コーン交差法による点列の折れ線化 | |
| INT FVALGAPI | fnFIE_cg_vectorize2d_dp (const PNT_T *src, UINT num_src, PNT_T *dst, UINT *index, UINT *num_dst, DOUBLE threshold) |
| DP法による点列の折れ線化 | |
| INT FVALGAPI | fnFIE_fit_centroid (const DPNT_T *pnts, INT pnt_num, enum f_fit_mode fitting_mode, DOUBLE param, DPNT_T *center) |
![[[OSS]]](oss.png) 点群からの重心座標推定 点群からの重心座標推定 | |
| INT FVALGAPI | fnFIE_fit_circle (const DPNT_T *pnts, INT pnt_num, enum f_fit_mode fitting_mode, DOUBLE param, DPNT_T *center, DOUBLE *radius) |
![[[OSS]]](oss.png) 点群からの円近似 点群からの円近似 | |
| INT FVALGAPI | fnFIE_fit_circle2 (const DPNT_T *pnts, INT pnt_num, enum f_fit_mode fitting_mode, DOUBLE param, DPNT_T *center, DOUBLE *radius) |
![[[OSS]]](oss.png) 点群からの円近似 点群からの円近似 | |
| INT FVALGAPI | fnFIE_fit_ellipse_b2ac (const DPNT_T *points, INT num, DOUBLE *cx, DOUBLE *cy, DOUBLE *major, DOUBLE *minor, DOUBLE *theta) |
![[[OSS]]](oss.png) 点列からの楕円の最小二乗近似 点列からの楕円の最小二乗近似 | |
| INT FVALGAPI | fnFIE_fit_ellipse (const DPNT_T *pnts, INT pnt_num, enum f_fit_mode fitting_mode, DOUBLE param, DPNT_T *center, DOUBLE *major, DOUBLE *minor, DOUBLE *theta) |
![[[OSS]]](oss.png) 点群からの楕円近似 点群からの楕円近似 | |
| INT FVALGAPI | fnFIE_fit_line (const DPNT_T *pnts, INT pnt_num, enum f_fit_mode fitting_mode, DOUBLE param, DLINE_T *line) |
![[[OSS]]](oss.png) 点群からの直線近似 点群からの直線近似 | |
| INT FVALGAPI | fnFIE_fit_polynomial (const DPNT_T *pnts, UINT pnt_num, UINT degree, enum f_fit_mode fitting_mode, DOUBLE param, DOUBLE *coefficient) |
![[[OSS]]](oss.png) 点群からのn次多項式近似 点群からのn次多項式近似 | |
列挙型
| enum f_pfit_calc_mode |
点群マッチングの処理選択
点群マッチングの処理方法は、以下の3種類となります。
- 最小二乗法
- ロバスト推定
- ミニマックス近似
はじめに、点群マッチングの概要を説明します。
ふたつの点群 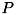 と
と  があり、それらの点どうしの対応がとれているものとします。 また、点群
があり、それらの点どうしの対応がとれているものとします。 また、点群 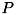 ,
, は誤差を除けば相似であるとします。 このとき、点群
は誤差を除けば相似であるとします。 このとき、点群 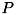 に対して、平行移動(
に対して、平行移動(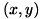 )、重心まわりの回転(
)、重心まわりの回転(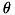 ) および 重心基準のスケーリング(拡大・縮小)(
) および 重心基準のスケーリング(拡大・縮小)( ) を施し、点群
) を施し、点群  に重ね合わせることを考えます。
に重ね合わせることを考えます。
点群マッチングでは、このときの最適なパラメータ 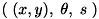 を求めます。
を求めます。
その際の‘最適’の基準として、「最小二乗法」と「ミニマックス近似」を用意しました。 なお,「ロバスト推定」は、点群内のはずれ値(他と比べて誤差の大きい点)を除いて最小二乗法を行うものです。
さて、最小二乗法とミニマックス近似の違いは次のとおりです。
あるパラメータ 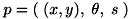 における、 点群の
における、 点群の 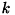 番目の対応点での誤差(対応点間のユークリッド距離)を
番目の対応点での誤差(対応点間のユークリッド距離)を 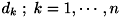 とします。 このとき、誤差ベクトル
とします。 このとき、誤差ベクトル 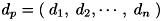 に対して、その大きさ(ノルム)を次のように定義します。
に対して、その大きさ(ノルム)を次のように定義します。
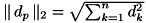 (ユークリッドノルム)
(ユークリッドノルム)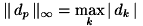 (最大値ノルム)
(最大値ノルム)
すると、最小二乗法とミニマックス近似はそれぞれ,これらのノルムに対して最小化を行ったものになります。
- 最小二乗法
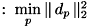
- ミニマックス近似
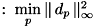
具体例として、4点のマッチング例を下図に示します。 この図では、合わされる点群  を緑色点で表し、合わせる点群
を緑色点で表し、合わせる点群 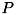 の最小二乗解を青色点、 ミニマックス近似解を赤色点で表しています。 また、橙色円は、ミニマックス近似解における最大誤差を半径とする円です。
の最小二乗解を青色点、 ミニマックス近似解を赤色点で表しています。 また、橙色円は、ミニマックス近似解における最大誤差を半径とする円です。
| enum f_fit_mode |
関数
| INT FVALGAPI fnFIE_pfit_coord | ( | INT | iPntNum, | |
| DPNT_T | taOldPnt[], | |||
| DPNT_T | taNewPnt[], | |||
| DOUBLE | dSigmaCoef, | |||
| enum f_pfit_calc_mode | iCalcMode, | |||
| DOUBLE * | dpXc, | |||
| DOUBLE * | dpYc, | |||
| DOUBLE * | dpTheta, | |||
| DOUBLE * | dpScale | |||
| ) |
点群マッチングによる座標系パラメータ(原点座標,傾きおよびスケール)の算出
新座標系上の座標値群を旧座標系上の座標値群に 最小二乗法,ロバスト推定 または ミニマックス近似 によりマッチングします. その際,新座標系上の座標値群と旧座標系上の座標値群の各点は配列要素順に対応づけがあるものとします. 結果出力は,旧座標系から見た新座標系のパラメータ(原点座標,傾きおよびスケール)です.
ロバスト推定用重みしきい値の係数は,入力データの誤差(ばらつき)の標準偏差に掛ける係数を入力します. 例えば,3σをしきい値にする場合はσの係数である‘3’を入力します.
ミニマックス近似では,各対応点の距離(誤差)の最大値が最も小さくなるように合わせ込みを行います.
- 引数:
-
[in] iPntNum データ(座標)点の数(2点以上) [in] taOldPnt[] 旧座標系上の座標値群(合わされる方) [in] taNewPnt[] 新座標系上の座標値群(合わせる方) [in] dSigmaCoef ロバスト推定用重みしきい値の係数 [in] iCalcMode 処理選択 - F_PFIT_LSQ 最小二乗法:スケール推定なし
- F_PFIT_LSQ_SCALE 最小二乗法:スケール推定あり
- F_PFIT_RBST ロバスト推定:スケール推定なし
- F_PFIT_RBST_SCALE ロバスト推定:スケール推定あり
- F_PFIT_MINMAX ミニマックス近似:スケール推定なし
- F_PFIT_MINMAX_SCALE ミニマックス近似:スケール推定あり
[out] *dpXc 旧座標系から見た新座標系の原点x座標 [out] *dpYc 旧座標系から見た新座標系の原点y座標 [out] *dpTheta 旧座標系から見た新座標系の傾き(rad:[-π,π]) [out] *dpScale 旧座標系から見た新座標系のスケール(相似比)(処理選択で‘スケール推定なし’を選択した場合は、1.0 が返ります。)
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_NOMEMORY メモリ確保失敗 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_CALC_IMPOSSIBLE ロバスト推定失敗(重みしきい値が小さくなりすぎた)または ミニマックス近似失敗(反復回数オーバー) F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
| INT FVALGAPI fnFIE_pfit_points | ( | INT | iPntNum, | |
| DPNT_T | taWork[], | |||
| DPNT_T | taMaster[], | |||
| DOUBLE | dSigmaCoef, | |||
| enum f_pfit_calc_mode | iCalcMode, | |||
| DPNT_T | taConv[], | |||
| DOUBLE | daErr[] | |||
| ) |
点群マッチング後の座標値および誤差の算出
同一座標系上の点群(Master&Work)に対し,最小二乗法,ロバスト推定 または ミニマックス近似 により, Master点群をWork点群にマッチングします. その際,Master点群とWork点群の各点は配列要素順に対応づけがあるものとします. 結果出力は,マッチング後のMaster各点の位置と,それらの対応するWork各点との距離(誤差)です.
ロバスト推定用重みしきい値の係数は,入力データの誤差(ばらつき)の標準偏差に掛ける係数を入力します. 例えば,3σをしきい値にする場合はσの係数である‘3’を入力します.
ミニマックス近似では,各対応点の距離(誤差)の最大値が最も小さくなるように合わせ込みを行います.
- 引数:
-
[in] iPntNum データ(座標)点の数(2点以上) [in] taWork[] ワーク点群座標データ(合わされる方) [in] taMaster[] マスタ点群座標データ(合わせる方) [in] dSigmaCoef ロバスト推定用重みしきい値の係数 [in] iCalcMode 処理選択 - F_PFIT_LSQ 最小二乗法:スケール推定なし
- F_PFIT_LSQ_SCALE 最小二乗法:スケール推定あり
- F_PFIT_RBST ロバスト推定:スケール推定なし
- F_PFIT_RBST_SCALE ロバスト推定:スケール推定あり
- F_PFIT_MINMAX ミニマックス近似:スケール推定なし
- F_PFIT_MINMAX_SCALE ミニマックス近似:スケール推定あり
[out] taConv[] マッチング後のマスタ点群の座標(taMaster[] と同じでもよい) [out] daErr[] マッチング後の対応する2点間の距離(誤差)
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_NOMEMORY メモリ確保失敗 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_CALC_IMPOSSIBLE ロバスト推定失敗(重みしきい値が小さくなりすぎた)または ミニマックス近似失敗(反復回数オーバー) F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
| INT FVALGAPI fnFIE_pfit_param | ( | INT | iPntNum, | |
| DPNT_T | taWork[], | |||
| DPNT_T | taMaster[], | |||
| DOUBLE | dSigmaCoef, | |||
| enum f_pfit_calc_mode | iCalcMode, | |||
| DOUBLE * | dpXcOrg, | |||
| DOUBLE * | dpYcOrg, | |||
| DOUBLE * | dpXc, | |||
| DOUBLE * | dpYc, | |||
| DOUBLE * | dpTheta, | |||
| DOUBLE * | dpScale | |||
| ) |
点群マッチングの変換パラメータ(重心,回転角およびスケール)算出
同一座標系上の点群(Master&Work)に対し,最小二乗法,ロバスト推定 または ミニマックス近似 により, Master点群をWork点群にマッチングします. その際,Master点群とWork点群の各点は配列要素順に対応づけがあるものとします. 結果出力は,マッチング後のMaster点群の重心と,その周りの回転角およびスケール(相似比)です.
ロバスト推定用重みしきい値の係数は,入力データの誤差(ばらつき)の標準偏差に掛ける係数を入力します. 例えば,3σをしきい値にする場合はσの係数である‘3’を入力します.
ミニマックス近似では,各対応点の距離(誤差)の最大値が最も小さくなるように合わせ込みを行います.
- 引数:
-
[in] iPntNum データ(座標)点の数(2点以上) [in] taWork[] ワーク点群座標データ(合わされる方) [in] taMaster[] マスタ点群座標データ(合わせる方) [in] dSigmaCoef ロバスト推定用重みしきい値の係数 [in] iCalcMode 処理選択 - F_PFIT_LSQ 最小二乗法:スケール推定なし
- F_PFIT_LSQ_SCALE 最小二乗法:スケール推定あり
- F_PFIT_RBST ロバスト推定:スケール推定なし
- F_PFIT_RBST_SCALE ロバスト推定:スケール推定あり
- F_PFIT_MINMAX ミニマックス近似:スケール推定なし
- F_PFIT_MINMAX_SCALE ミニマックス近似:スケール推定あり
[out] *dpXcOrg 元の(マッチング前の)マスタ点群の重心x座標 [out] *dpYcOrg 元の(マッチング前の)マスタ点群の重心y座標 [out] *dpXc マッチング後のマスタ点群の重心x座標 [out] *dpYc マッチング後のマスタ点群の重心y座標 [out] *dpTheta マスタ点群の重心周りの回転角(rad:[-π,π]) [out] *dpScale マスタ点群のスケール(相似比)(処理選択で‘スケール推定なし’を選択した場合は、1.0 が返ります。)
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_NOMEMORY メモリ確保失敗 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_CALC_IMPOSSIBLE ロバスト推定失敗(重みしきい値が小さくなりすぎた)または ミニマックス近似失敗(反復回数オーバー) F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
| INT FVALGAPI fnFIE_cg_vectorize2d_cone | ( | const PNT_T * | src, | |
| UINT | num_src, | |||
| PNT_T * | dst, | |||
| UINT * | index, | |||
| UINT * | num_dst, | |||
| DOUBLE | radius | |||
| ) |
コーン交差法による点列の折れ線化
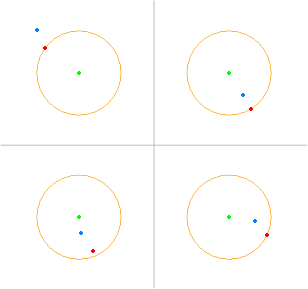
コーン交差法(Cone Intersection Method)を用いて、点列を間引いて折れ線にします。 入力点列の始点と終点は必ず出力します。 結果は元の点列のうち有効な点の場所を示すインデックス配列と、 有効な点の座標を並べた点列の2種類で出力します。
fnFIE_measure_get_boundary() で作成した2値ブローブの境界点列を入力することを想定しています。 fnFIE_region_calc_boundary_ex() や fnFIE_region_calc_boundary() で作成した点列の場合、配列の先頭から最初のストッパ(I32_MINを格納した点)までの先頭の点列のみ処理を行います。 ストッパは無くてもかまいません。また、閉曲線になっている必要もありません。
- アルゴリズム
コーン交差法のアルゴリズム
- 処理例
下図は境界点列を赤色で表現したものです。点列の点数は3042点です。radius が 1.0の時、折れ線化の結果は以下の矢印になります。点列の座標点数は78点です。
処理前の点列
radius が 4.0の時、折れ線化の結果は以下の矢印になります。点列の座標点数は54点です。
処理後の点列 誤差円半径1.0

処理後の点列 誤差円半径4.0
- 引数:
-
[in] src 入力座標点列 [in] num_src 入力座標点列のサイズ。 3点以上を与えてください。 [out] dst 出力座標点列。 num_src 以上の大きさを持つ配列を与えてください。 不要な場合はNULLを与えてください。 [out] index 出力座標のインデックス配列。折れ線を src での先頭からのオフセットで表現します。 num_src 以上の大きさを持つ配列を与えてください。不要な場合はNULLを与えてください。 [out] num_dst 出力座標点列のサイズ [in] radius 誤差円の半径。 ゼロより大きい値を与えてください。 入力点列の座標が整数のため、0.5以下では間引きの効果はほとんど無くなります。 大きくすると元の点列と出力する折れ線の乖離が大きくなります。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_NOMEMORY メモリ不足 F_ERR_INVALID_PARAM パラメータ異常 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
| INT FVALGAPI fnFIE_cg_vectorize2d_dp | ( | const PNT_T * | src, | |
| UINT | num_src, | |||
| PNT_T * | dst, | |||
| UINT * | index, | |||
| UINT * | num_dst, | |||
| DOUBLE | threshold | |||
| ) |
DP法による点列の折れ線化
点列をDP法( Ramer / Douglas Peucker algorithm )を用いて間引き、折れ線にして出力します。 始点と終点が異なる点列を与えた場合は、始点と終点を必ず出力します。 始点と終点に同じ座標の入った点列を与えた場合、 閉曲線と判断して入力点列の始点から最も遠い点を探し、その点から最も遠い点を探して新しい始点としてから折れ線化するため 必ずしも入力点列の始点と終点を出力するとは限りませんが、 出力点列の始点と終点には同一の座標が入ります。
fnFIE_measure_get_boundary() で作成した2値ブローブの境界点列を入力することを想定しています。 fnFIE_region_calc_boundary_ex() や fnFIE_region_calc_boundary() で作成した点列の場合、配列の先頭から最初のストッパ(I32_MINを格納した点)までの先頭の点列のみ処理を行います。 ストッパは無くてもかまいません。また、閉曲線になっている必要もありません。
- アルゴリズム
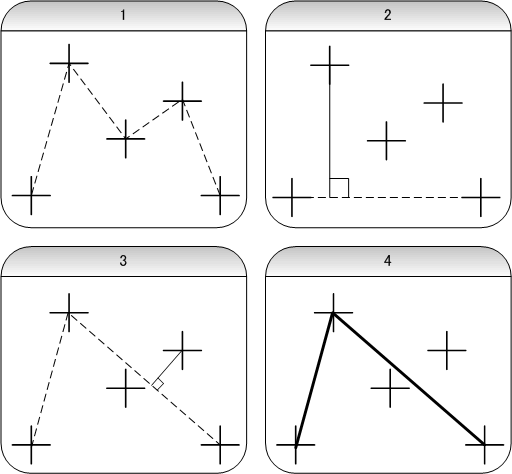
DP法のアルゴリズム
- 1.点列を用意します。
- 2.始点と終点を結ぶ線分を引き、最も遠い点から垂線をおろして長さを測ります。
- 3.垂線の長さが threshold より長かったらその点で線分を折り、残りの点のうち新たな線分から最も遠い点から垂線をおろして長さを測ります。
- 4.垂線の長さが threshold より短くなったら終了します。
- 処理例
- 下図は境界点列を赤色で表現したものです。点列の座標点数は3042点です。 threshold が 2.0の時、折れ線化の結果は以下の矢印になります。点列の座標点数は73点です。

処理前の点列
threshold が 24.0の時、折れ線化の結果は以下の矢印になります。点列の座標点数は38点です。
処理後の点列 閾値2.0
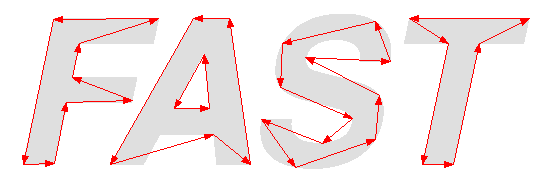
処理後の点列 閾値24.0
- 引数:
-
[in] src 入力座標点列 [in] num_src 入力座標点列のサイズ。3点以上を与えてください。 [out] dst 出力座標点列。 num_src 以上の大きさを持つ配列を与えてください。不要な場合はNULLを与えてください。 [out] index 出力座標点列のインデックス配列。出力座標点列を src の先頭からのオフセットで表現したものです。 num_src 以上の大きさを持つ配列を与えてください。不要な場合はNULLを与えてください。 [out] num_dst 出力座標点列のサイズ [in] threshold 折れ線閾値。ゼロより大きい値を与えてください。 折れ線と点列を比較したとき点列が折れ線の方向から垂直に何ピクセル外れていたら折るかを指定します。 出力する点列は元の点列から threshold より大きく外れません。
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM パラメータ異常 F_ERR_NOMEMORY メモリ不足 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- Urs Ramer, "An iterative procedure for the polygonal approximation of plane curves", Computer Graphics and Image Processing, vol. 1, pp. 244-256, 1972.
- DAVID H DOUGLAS, THOMAS K PEUCKER, "ALGORITHMS FOR THE REDUCTION OF THE NUMBER OF POINTS REQUIRED TO REPRESENT A DIGITIZED LINE OR ITS CARICATURE", Cartographica: The International Journal for Geographic Information and Geovisualization, Volume 10, pp.112-122, Number 2 / December 1973.
| INT FVALGAPI fnFIE_fit_centroid | ( | const DPNT_T * | pnts, | |
| INT | pnt_num, | |||
| enum f_fit_mode | fitting_mode, | |||
| DOUBLE | param, | |||
| DPNT_T * | center | |||
| ) |
![[[OSS]]](oss.png) 点群からの重心座標推定
点群からの重心座標推定
与えれた座標点群から、最小二乗法または、ロバスト推定法で点群の重心座標を算出します。
- 最適化パラメータ( param )
誤差の計算式は、以下の通りとなります。
![\[ \epsilon _{i} = \sqrt{ ( x _{i} - cx ) ^{2} + ( y _{i} - cy ) ^{2} } \]](form_994.png)
なお、 cx は重心のx座標、 cy は重心のy座標となります。
F_FIT_MESTIMATOR を指定した場合、 param は 誤差 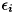 の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。
の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。
F_FIT_MESTIMATOR2 を指定した場合、param は 誤差 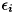 の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
- 90%信頼区間内:1.645
- 95%信頼区間内:1.960
- 99%信頼区間内:2.567
- 99.9%信頼区間内:3.291
入力点群の個数( pnt_num )が 1 の場合は、単に入力座標を重心座標として出力する処理となります。 また、 2 の場合は2点の中点座標を返します。
- 引数:
-
[in] pnts 入力点群 [in] pnt_num 入力点群の個数( pnt_num >= 1 ) [in] fitting_mode 近似モード - F_FIT_LSM 最小二乗法
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…自動決定される標準偏差の係数を設定可能
[in] param 最適化パラメータ(ロバスト推定法で利用) [out] center 点群の重心座標
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM 不正なパラメータが入力された F_ERR_NOMEMORY メモリ不足 F_ERR_CALC_IMPOSSIBLE 計算不可 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- David A. Forsyth, Jean Ponce, コンピュータビジョン §15.5, p391, 共立出版, 2007.
| INT FVALGAPI fnFIE_fit_circle | ( | const DPNT_T * | pnts, | |
| INT | pnt_num, | |||
| enum f_fit_mode | fitting_mode, | |||
| DOUBLE | param, | |||
| DPNT_T * | center, | |||
| DOUBLE * | radius | |||
| ) |
![[[OSS]]](oss.png) 点群からの円近似
点群からの円近似
与えれた座標点群から、最小二乗法または、ロバスト推定法で円の中心座標と半径を算出します。
- 最適化パラメータ( param )
誤差の計算式は、以下の通りとなります。
![\[ \epsilon _{i} = | ( x _{i} - cx ) ^{2} + ( y _{i} - cy ) ^{2} - r ^{2} | \]](form_996.png)
なお、 cx は中心x座標、 cy は中心y座標、 r は半径となります。
F_FIT_MESTIMATOR または、 F_FIT_RANSAC を指定した場合、 param は 誤差 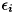 の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 近似しようとする円の半径がおおむね r であり座標点群のほぼ全てが円の半径から s ピクセル以内に収まると期待するとき、 s(s+2r)/2 を param に設定します。param の設定が難しい場合は fnFIE_fit_circle2() をご利用ください。
の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 近似しようとする円の半径がおおむね r であり座標点群のほぼ全てが円の半径から s ピクセル以内に収まると期待するとき、 s(s+2r)/2 を param に設定します。param の設定が難しい場合は fnFIE_fit_circle2() をご利用ください。
F_FIT_LMEDS を指定した場合は、 param は無視されます。 計算結果より自動的に標準偏差を計算します。 標準偏差より95%信頼区間内の点をインライアと判定します。
F_FIT_MESTIMATOR2 または、 F_FIT_LMEDS2 を指定した場合、param は 誤差 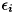 の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
- 90%信頼区間内:1.645
- 95%信頼区間内:1.960
- 99%信頼区間内:2.567
- 99.9%信頼区間内:3.291
- 入力点群の個数制限
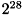 を満たさなければならないという制限があります。 この制限は、内部計算で行列演算を用いていることに起因します。
を満たさなければならないという制限があります。 この制限は、内部計算で行列演算を用いていることに起因します。
- 乱数
- 引数:
-
[in] pnts 入力点群 [in] pnt_num 入力点群の個数( pnt_num >= 3 ) [in] fitting_mode 近似モード - F_FIT_LSM 最小二乗法
- F_FIT_LSM_FAST 最小二乗法(旧ライブラリ仕様)
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_RANSAC ロバスト推定法(ランザック法)
- F_FIT_LMEDS ロバスト推定法(最小メディアン法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…標準偏差を自動決定
- F_FIT_LMEDS2 ロバスト推定法(最小メディアン法)…自動決定される標準偏差の係数を設定可能
[in] param 最適化パラメータ(ロバスト推定法で利用) [out] center 円の中心座標 [out] radius 円の半径
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM 不正なパラメータが入力された F_ERR_NOMEMORY メモリ不足 F_ERR_CALC_IMPOSSIBLE 計算不可 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- M. A. Fischler, R. C. Bolles, Random Sample Consensus : A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Commun. ACM, no.24, vol.6, pp.381-395, 1981.
- Rousseeuw P. J, Least Median of Squares Regression, Journal of the American Statistical Association, 79, pp.871-880, 1984.
- David A. Forsyth, Jean Ponce, コンピュータビジョン §15.5, 共立出版, 2007.
- 松山隆司 他, コンピュータビジョン 第3章, 新技術コミュニケーションズ, 1998.
- D. Umbach, K.N. Jones, A Few Methods for Fitting Circles to Data, IEEE Transactions on Instrumentation and Measurement, 2000.
- 使用例:
// エラー処理は省略しているので注意して下さい。 #include "fie.h" #include "oal_aloc.h" //メモリ管理 #include <math.h> #define WIDTH 256 //出力画像の幅 #define HEIGHT 256 //出力画像の高さ #define PNTS_NUM 256 //入力点数 #define PER 1 //円周の何%に点群を配置するか(1で全周) VOID fit_circle() { INT i; //ループ用変数 DOUBLE val = 0; //画像に描画する際の濃度値 //ルート画像 FHANDLE hdst = NULL; //結果画像 //チャイルド画像 FHANDLE hrgb_r = NULL; //R画像 FHANDLE hrgb_g = NULL; //G画像 FHANDLE hrgb_b = NULL; //B画像 F_RANDDESC r; //擬似乱数列生成用データ UINT seed = 1324; //乱数因子(適当な値) DOUBLE random; //乱数 //近似円生成パラメータ DPNT_T f_center; //近似円の中心座標 DOUBLE f_radius; //近似円の半径 //点列の作成 DPNT_T * pnts = NULL; //円のノイズ付加点群生成パラメータ DOUBLE radius = 100; //半径 DOUBLE radian = PI; //角度 DPNT_T center; center.x = WIDTH/2; //画像中心X座標 center.y = HEIGHT/2; //画像中心Y座標 //乱数生成子の初期化 fnFIE_mtrand_init(seed, &r); //点列領域確保 pnts = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * PNTS_NUM); //出力画像の領域を確保します hdst = fnFIE_img_root_alloc( F_IMG_UC8, 3, WIDTH, HEIGHT ); //チャイルド画像の領域を確保する hrgb_r = fnFIE_img_child_alloc_single_ch(hdst, 0, 0, 0, WIDTH, HEIGHT); hrgb_g = fnFIE_img_child_alloc_single_ch(hdst, 1, 0, 0, WIDTH, HEIGHT); hrgb_b = fnFIE_img_child_alloc_single_ch(hdst, 2, 0, 0, WIDTH, HEIGHT); //出力画像を白色(255)で塗りつぶす fnFIE_img_clear(hdst, 255); //入力点列の生成 for(i = 0; i < PNTS_NUM; i++) { radian += ((2 * PI) * (PER))/PNTS_NUM; //角度 pnts[i].x = center.x + (radius * cos(radian) ); //X座標 pnts[i].y = center.y + (radius * sin(radian) ); //Y座標 //乱数の生成 random = fnFIE_mtrand_real2(&r); //X座標に乱数を付加 pnts[i].x += 100 * (random - 0.5); //Y座標に乱数を付加 pnts[i].y += 100 * (random - 0.5); //点列を描画する(点描画では小さいので,円で描画) fnFIE_draw_circle(hdst, &val, F_DRAW_FILL_IN, pnts[i], 1); } //近似円の計算(M推定法…標準偏差の自動決定) fnFIE_fit_circle(pnts, PNTS_NUM, F_FIT_MESTIMATOR2, 1.645, &f_center, &f_radius); //近似円を描画する fnFIE_draw_circle(hrgb_g, &val, F_DRAW_LINE, f_center, f_radius); fnFIE_draw_circle(hrgb_b, &val, F_DRAW_LINE, f_center, f_radius); //近似円の計算(最小二乗法) fnFIE_fit_circle(pnts, PNTS_NUM, F_FIT_LSM_FAST, 0, &f_center, &f_radius); //近似円を描画する fnFIE_draw_circle(hrgb_r, &val, F_DRAW_LINE, f_center, f_radius); fnFIE_draw_circle(hrgb_g, &val, F_DRAW_LINE, f_center, f_radius); //画像をPNG形式で保存する fnFIE_save_png("result.png", hdst, -1); //解放 fnOAL_free(pnts); fnFIE_free_object(hdst); fnFIE_free_object(hrgb_r); fnFIE_free_object(hrgb_g); fnFIE_free_object(hrgb_b); } INT main(VOID) { // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); fit_circle(); // 終了処理 fnFIE_teardown(); return 0; }
- 処理結果例:

処理結果画像
| INT FVALGAPI fnFIE_fit_circle2 | ( | const DPNT_T * | pnts, | |
| INT | pnt_num, | |||
| enum f_fit_mode | fitting_mode, | |||
| DOUBLE | param, | |||
| DPNT_T * | center, | |||
| DOUBLE * | radius | |||
| ) |
![[[OSS]]](oss.png) 点群からの円近似
点群からの円近似
与えれた座標点群から、最小二乗法または、ロバスト推定法で円の中心座標と半径を算出します。
- 最適化パラメータ( param )
誤差の計算式は、以下の通りとなります。
![\[ \epsilon _{i} = | \sqrt{ ( x _{i} - cx ) ^{2} + ( y _{i} - cy ) ^{2} } - r | \]](form_998.png)
なお、 cx は中心x座標、 cy は中心y座標、 r は半径となります。
F_FIT_MESTIMATOR または、 F_FIT_RANSAC を指定した場合、 param は 誤差 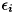 の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
F_FIT_LMEDS を指定した場合は、 param は無視されます。 計算結果より自動的に標準偏差を計算します。 標準偏差より95%信頼区間内の点をインライアと判定します。
F_FIT_MESTIMATOR2 または、 F_FIT_LMEDS2 を指定した場合、param は 誤差 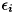 の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
- 90%信頼区間内:1.645
- 95%信頼区間内:1.960
- 99%信頼区間内:2.567
- 99.9%信頼区間内:3.291
- 入力点群の個数制限
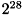 を満たさなければならないという制限があります。 この制限は、内部計算で行列演算を用いていることに起因します。
を満たさなければならないという制限があります。 この制限は、内部計算で行列演算を用いていることに起因します。
- 乱数
- 引数:
-
[in] pnts 入力点群 [in] pnt_num 入力点群の個数( pnt_num >= 3 ) [in] fitting_mode 近似モード - F_FIT_LSM 最小二乗法
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_RANSAC ロバスト推定法(ランザック法)
- F_FIT_LMEDS ロバスト推定法(最小メディアン法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…標準偏差を自動決定
- F_FIT_LMEDS2 ロバスト推定法(最小メディアン法)…自動決定される標準偏差の係数を設定可能
[in] param 最適化パラメータ(ロバスト推定法で利用) [out] center 円の中心座標 [out] radius 円の半径
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM 不正なパラメータが入力された F_ERR_NOMEMORY メモリ不足 F_ERR_CALC_IMPOSSIBLE 計算不可 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- M. A. Fischler, R. C. Bolles, Random Sample Consensus : A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Commun. ACM, no.24, vol.6, pp.381-395, 1981.
- Rousseeuw P. J, Least Median of Squares Regression, Journal of the American Statistical Association, 79, pp.871-880, 1984.
- David A. Forsyth, Jean Ponce, コンピュータビジョン §15.5, 共立出版, 2007.
- 松山隆司 他, コンピュータビジョン 第3章, 新技術コミュニケーションズ, 1998.
- D. Umbach, K.N. Jones, A Few Methods for Fitting Circles to Data, IEEE Transactions on Instrumentation and Measurement, 2000.
| INT FVALGAPI fnFIE_fit_ellipse_b2ac | ( | const DPNT_T * | points, | |
| INT | num, | |||
| DOUBLE * | cx, | |||
| DOUBLE * | cy, | |||
| DOUBLE * | major, | |||
| DOUBLE * | minor, | |||
| DOUBLE * | theta | |||
| ) |
![[[OSS]]](oss.png) 点列からの楕円の最小二乗近似
点列からの楕円の最小二乗近似
- 非推奨:
- 本関数は後方互換性のために残されています。
新規の開発では fnFIE_fit_ellipse() を使用し、本関数は使用しないでください。
本関数では Andrew W. Fitzgibbon らのB2AC手法を用い楕円の当てはめを 行います。本手法では座標点群が偏っている場合や ノイズの多い状況において、弊社従来手法と比較して 計算不能に陥りにくく、より妥当な計算結果を得ることができます。
- 引数:
-
[in] points 入力点群配列 [in] num 入力点数 ( points の要素数, 5以上) [out] cx 楕円の中心X座標 [out] cy 楕円の中心Y座標 [out] major 楕円の主軸半径 [out] minor 楕円の副軸半径 [out] theta 楕円の主軸角度( -PI / 2 ≦theta ≦ +PI / 2 )
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_NOMEMORY メモリ不足 F_ERR_INVALID_PARAM パラメータ不正 F_ERR_CALC_IMPOSSIBLE 計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- Andrew W. Fitzgibbon, Maurizio Pilu, and Robert B. Fisher \ Direct least-squares fitting of ellipses, \ IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(5), pp.476~480, May 1999
| INT FVALGAPI fnFIE_fit_ellipse | ( | const DPNT_T * | pnts, | |
| INT | pnt_num, | |||
| enum f_fit_mode | fitting_mode, | |||
| DOUBLE | param, | |||
| DPNT_T * | center, | |||
| DOUBLE * | major, | |||
| DOUBLE * | minor, | |||
| DOUBLE * | theta | |||
| ) |
![[[OSS]]](oss.png) 点群からの楕円近似
点群からの楕円近似
与えれた座標点群から、最小二乗法または、ロバスト推定法で楕円の中心座標、主軸半径、副軸半径、そして主軸角度を算出します。
なお、 fitting_mode に F_FIT_LSM を指定した場合は、 fnFIE_fit_ellipse_b2ac() が使用されます。 また、各ロバスト推定法を指定した場合も、 fnFIE_fit_ellipse_b2ac() と同じアルゴリズムを使用した関数、または、 fnFIE_fit_ellipse_b2ac() を一部改良した関数が使用されます。
- 最適化パラメータ( param )
誤差の計算式は、楕円を2次曲線の式 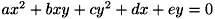 で表すと、 以下の通りとなります。
で表すと、 以下の通りとなります。
![\[ \epsilon _{i} = | ax _{i} ^{2} + bx _{i} y _{i} + cy _{i} ^{2} + dx _{i} + ey _{i} | \]](form_1000.png)
F_FIT_MESTIMATOR または、 F_FIT_RANSAC を指定した場合、 param は 誤差 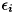 の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
F_FIT_LMEDS を指定した場合は、 param は無視されます。 計算結果より自動的に標準偏差を計算します。 標準偏差より95%信頼区間内の点をインライアと判定します。
F_FIT_MESTIMATOR2 または、 F_FIT_LMEDS2 を指定した場合、param は 誤差 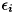 の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
- 90%信頼区間内:1.645
- 95%信頼区間内:1.960
- 99%信頼区間内:2.567
- 99.9%信頼区間内:3.291
- 入力点群の個数制限
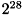 を満たさなければならないという制限があります。 この制限は、内部計算で行列演算を用いていることに起因します。
を満たさなければならないという制限があります。 この制限は、内部計算で行列演算を用いていることに起因します。
- 乱数
- 引数:
-
[in] pnts 入力点群 [in] pnt_num 入力点群の個数( pnt_num >= 5 ) [in] fitting_mode 近似モード - F_FIT_LSM 最小二乗法
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_RANSAC ロバスト推定法(ランザック法)
- F_FIT_LMEDS ロバスト推定法(最小メディアン法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…標準偏差を自動決定
- F_FIT_LMEDS2 ロバスト推定法(最小メディアン法)…自動決定される標準偏差の係数を設定可能
[in] param 最適化パラメータ(ロバスト推定法で利用) [out] center 楕円の中心点 [out] major 楕円の主軸半径 [out] minor 楕円の副軸半径 [out] theta 楕円の主軸角度( -PI / 2 ≦ theta ≦ +PI / 2 )
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM 不正なパラメータが入力された F_ERR_NOMEMORY メモリ不足 F_ERR_CALC_IMPOSSIBLE 計算不可 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- M. A. Fischler, R. C. Bolles, Random Sample Consensus : A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Commun. ACM, no.24, vol.6, pp.381-395, 1981.
- Rousseeuw P. J, Least Median of Squares Regression, Journal of the American Statistical Association, 79, pp.871-880, 1984.
- Andrew W. Fitzgibbon, Maurizio Pilu, and Robert B. Fisher, Direct least-squares fitting of ellipses, IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(5), pp.476-480, May 1999.
- David A. Forsyth, Jean Ponce, コンピュータビジョン §15.5, 共立出版, 2007.
- 松山隆司 他, コンピュータビジョン 第3章, 新技術コミュニケーションズ, 1998.
- 使用例:
// エラー処理は省略しているので注意して下さい。 #include "fie.h" #include "oal_aloc.h" //メモリ管理 #include <math.h> #define WIDTH 256 //出力画像の幅 #define HEIGHT 256 //出力画像の高さ #define PNTS_NUM 128 //入力点数 #define PER 0.5 //円周の何%に点群を配置するか(1で全周) VOID fit_circle() { INT i; //ループ用変数 DOUBLE val = 0; //画像に描画する際の濃度値 //ルート画像 FHANDLE hdst = NULL; //結果画像 //チャイルド画像 FHANDLE hrgb_r = NULL; //R画像 FHANDLE hrgb_g = NULL; //G画像 FHANDLE hrgb_b = NULL; //B画像 F_RANDDESC r; //擬似乱数列生成用データ UINT seed = 777; //乱数因子(適当な値) DOUBLE random; //乱数 //近似楕円生成パラメータ DPNT_T f_center; //中心座標 DOUBLE f_major; //長軸 DOUBLE f_minor; //短軸 DOUBLE f_theta; //回転角 //点列の作成 DPNT_T * pnts = NULL; //楕円のノイズ付加点群生成パラメータ DOUBLE major = 100; //長軸 DOUBLE minor = 80; //短軸 DOUBLE radian = PI; //角度 DPNT_T center; //中心座標 center.x = WIDTH/2; //画像中心X座標 center.y = HEIGHT/2; //画像中心Y座標 //乱数生成子の初期化 fnFIE_mtrand_init(seed, &r); //点列領域確保 pnts = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * PNTS_NUM); //出力画像の領域を確保します hdst = fnFIE_img_root_alloc( F_IMG_UC8, 3, WIDTH, HEIGHT ); //チャイルド画像の領域を確保する hrgb_r = fnFIE_img_child_alloc_single_ch(hdst, 0, 0, 0, WIDTH, HEIGHT); hrgb_g = fnFIE_img_child_alloc_single_ch(hdst, 1, 0, 0, WIDTH, HEIGHT); hrgb_b = fnFIE_img_child_alloc_single_ch(hdst, 2, 0, 0, WIDTH, HEIGHT); //出力画像を白色(255)で塗りつぶす fnFIE_img_clear(hdst, 255); //入力点列の生成 for(i = 0; i < PNTS_NUM; i++) { radian += ((2 * PI) * (PER))/PNTS_NUM; //角度 pnts[i].x = center.x + (major * cos(radian) ); //X座標 pnts[i].y = center.y + (minor * sin(radian) ); //Y座標 //乱数の生成 random = fnFIE_mtrand_real2(&r); //X座標に乱数を付加 pnts[i].x += 5 * (random - 0.5); //Y座標に乱数を付加 pnts[i].y += 5 * (random - 0.5); //点列を描画する(点描画では小さいので,円で描画) fnFIE_draw_circle(hdst, &val, F_DRAW_FILL_IN, pnts[i], 1); } //近似楕円の計算(最小二乗法) fnFIE_fit_ellipse(pnts, PNTS_NUM, F_FIT_LSM, 0, &f_center, &f_major, &f_minor, &f_theta); //近似楕円を描画する fnFIE_draw_ellipse(hrgb_g, &val, F_DRAW_LINE, f_center, f_major, f_minor, f_theta); fnFIE_draw_ellipse(hrgb_b, &val, F_DRAW_LINE, f_center, f_major, f_minor, f_theta); //画像をPNG形式で保存する fnFIE_save_png("result.png", hdst, -1); //解放 fnOAL_free(pnts); fnFIE_free_object(hdst); fnFIE_free_object(hrgb_r); fnFIE_free_object(hrgb_g); fnFIE_free_object(hrgb_b); } INT main(VOID) { // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); fit_circle(); // 終了処理 fnFIE_teardown(); return 0; }
- 処理結果例:

処理結果画像
| INT FVALGAPI fnFIE_fit_line | ( | const DPNT_T * | pnts, | |
| INT | pnt_num, | |||
| enum f_fit_mode | fitting_mode, | |||
| DOUBLE | param, | |||
| DLINE_T * | line | |||
| ) |
![[[OSS]]](oss.png) 点群からの直線近似
点群からの直線近似
与えれた座標点群から、最小二乗法または、ロバスト推定法で直線の係数を算出します。 各手法の詳細については、 最小二乗法とロバスト推定法を参照してください。
- 最適化パラメータ( param )
誤差の計算式は、直線の式を ax+by+c=0 とすると、以下の通りとなります。
![\[ \epsilon _{i} = \frac{ | ax _{i} + by _{i} + c | }{ \sqrt{ a ^{2} + b ^{2} } } \]](form_1007.png)
F_FIT_MESTIMATOR または、 F_FIT_RANSAC を指定した場合、 param は 誤差 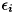 の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
F_FIT_LMEDS を指定した場合は、 param は無視されます。 計算結果より自動的に標準偏差を計算します。 標準偏差より95%信頼区間内の点をインライアと判定します。
F_FIT_MESTIMATOR2 または、 F_FIT_LMEDS2 を指定した場合、param は 誤差 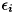 の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
- 90%信頼区間内:1.645
- 95%信頼区間内:1.960
- 99%信頼区間内:2.567
- 99.9%信頼区間内:3.291
- 乱数
なお、得られる直線は、傾きが [ -PI / 4 , PI / 4 ] または、 [ 3PI / 4 , 5PI / 4 ] の場合、 line->b を 1.0 に正規化します。 それ以外の傾きでは、 line->a を 1.0 に正規化します。
- 引数:
-
[in] pnts 入力点群 [in] pnt_num 入力点群の個数( pnt_num >= 2 ) [in] fitting_mode 近似モード - F_FIT_LSM 最小二乗法
- F_FIT_LSM_FAST 最小二乗法(旧ライブラリ仕様)
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_RANSAC ロバスト推定法(ランザック法)
- F_FIT_LMEDS ロバスト推定法(最小メディアン法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…標準偏差を自動決定
- F_FIT_LMEDS2 ロバスト推定法(最小メディアン法)…自動決定される標準偏差の係数を設定可能
[in] param 最適化パラメータ(ロバスト推定法で利用) [out] line 直線の係数
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM 不正なパラメータが入力された F_ERR_NOMEMORY メモリ不足 F_ERR_CALC_IMPOSSIBLE 計算不可 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- M. A. Fischler, R. C. Bolles, Random Sample Consensus : A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Commun. ACM, no.24, vol.6, pp.381-395, 1981.
- Rousseeuw P. J, Least Median of Squares Regression, Journal of the American Statistical Association, 79, pp.871-880, 1984.
- David A. Forsyth, Jean Ponce, コンピュータビジョン §15.5, 共立出版, 2007.
- 松山隆司 他, コンピュータビジョン 第3章, 新技術コミュニケーションズ, 1998.
- 使用例:
// エラー処理は省略しているので注意して下さい。 #include "fie.h" #include "oal_aloc.h" //メモリ管理 #define WIDTH 256 //出力画像の幅 #define HEIGHT 256 //出力画像の高さ #define PNTS_NUM 64 //入力点数 VOID fit_line() { INT i; //ループ用変数 DOUBLE val = 0; //画像に描画する際の濃度値 F_RANDDESC r; //擬似乱数列生成用データ UINT seed = 152; //乱数因子(適当な値); DOUBLE random; //乱数 DPNT_T * pnts = NULL; //点列の作成 DLINE_T line; //直線のパラメータ //ルート画像 FHANDLE hdst = NULL; //結果画像 //チャイルド画像 FHANDLE hrgb_r = NULL; //R画像 FHANDLE hrgb_g = NULL; //G画像 FHANDLE hrgb_b = NULL; //B画像 //乱数生成子の初期化 fnFIE_mtrand_init(seed, &r); //点列領域確保 pnts = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * PNTS_NUM); //出力画像の領域を確保します hdst = fnFIE_img_root_alloc( F_IMG_UC8, 3, WIDTH, HEIGHT ); //チャイルド画像の領域を確保する hrgb_r = fnFIE_img_child_alloc_single_ch(hdst, 0, 0, 0, WIDTH, HEIGHT); hrgb_g = fnFIE_img_child_alloc_single_ch(hdst, 1, 0, 0, WIDTH, HEIGHT); hrgb_b = fnFIE_img_child_alloc_single_ch(hdst, 2, 0, 0, WIDTH, HEIGHT); //出力画像を白色(255)で塗りつぶす fnFIE_img_clear(hdst, 255); //近似計算のための点列を生成 for( i = 0; i < PNTS_NUM; i++) { //座標の設定 pnts[i].x = i*(WIDTH/PNTS_NUM); //X座標 pnts[i].y = (2 * pnts[i].x) - 10; //Y座標 //乱数の生成 random = fnFIE_mtrand_real2(&r); //Y座標に乱数を付加 pnts[i].y += 200 * (random - 0.5); //点列を描画する fnFIE_draw_circle(hdst, &val, F_DRAW_FILL_IN, pnts[i], 1); } //最小二乗法による直線の推定 fnFIE_fit_line(pnts, PNTS_NUM, F_FIT_LSM, 0, &line); fnFIE_draw_line(hrgb_g, &val, line); fnFIE_draw_line(hrgb_b, &val, line); //ロバスト推定法(最小メディアン法)による直線の推定 fnFIE_fit_line(pnts, PNTS_NUM, F_FIT_LMEDS2, 1.0, &line); fnFIE_draw_line(hrgb_r, &val, line); fnFIE_draw_line(hrgb_g, &val, line); //画像をPNG形式で保存する fnFIE_save_png("result.png", hdst, -1); //解放 fnOAL_free(pnts); fnFIE_free_object(hdst); fnFIE_free_object(hrgb_r); fnFIE_free_object(hrgb_g); fnFIE_free_object(hrgb_b); } INT main(VOID) { // FIEライブラリの使用前に必ずコールする必要があります。 fnFIE_setup(); fit_line(); // 終了処理 fnFIE_teardown(); return 0; }
- 処理結果例:
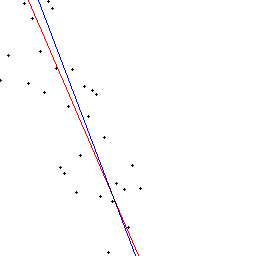
処理結果画像
| INT FVALGAPI fnFIE_fit_polynomial | ( | const DPNT_T * | pnts, | |
| UINT | pnt_num, | |||
| UINT | degree, | |||
| enum f_fit_mode | fitting_mode, | |||
| DOUBLE | param, | |||
| DOUBLE * | coefficient | |||
| ) |
![[[OSS]]](oss.png) 点群からのn次多項式近似
点群からのn次多項式近似
与えれた座標点群から、最小二乗法または、ロバスト推定法で、指定された次数のn次多項式 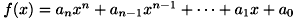 の係数を算出します。 各手法の詳細については、 最小二乗法とロバスト推定法を参照してください。 なお、ロバスト推定法については、現在以下のものについてのみ対応しています。
の係数を算出します。 各手法の詳細については、 最小二乗法とロバスト推定法を参照してください。 なお、ロバスト推定法については、現在以下のものについてのみ対応しています。
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_RANSAC ロバスト推定法(ランザック法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…標準偏差を自動決定
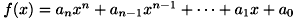 に対して、
に対して、 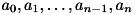 の順で格納されます。係数が0の項は、該当する箇所に0が格納されます。
の順で格納されます。係数が0の項は、該当する箇所に0が格納されます。coefficient へは、計算結果を格納するのに必要なサイズの配列を確保したうえで、その配列を渡してください。 その際、n次多項式で近似を行う場合、係数はn+1個であることに注意してください。 なお、エラー発生時は coefficient の内容は変更されません。
本関数で次数を1に設定した場合、1次多項式、つまり直線による近似を行います。しかし、 誤差の計算式等、内部的な処理に違いがあるため、 fnFIE_fit_line() とは異なる結果を返す場合があります。 直線による、より精度の高い近似を行いたい場合は、 fnFIE_fit_line() を使用してください。
本関数では、与えられた点群の各yの値と、指定された多項式との残差を最小化することで係数の算出を行います。 そのため、x軸に垂直な直線や、双曲線のように、1つのxに対して複数のf(x)が定義されるような曲線の近似はできません。 本来はそのような直線・曲線で近似されるような点群を入力した場合は、意図したような結果を得ることができませんので、 ご注意ください。
- 指定する次数の制限
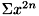 の数値演算を行う必要が あること、高次の多項式での近似を行うことによる誤差の増大に起因します。
の数値演算を行う必要が あること、高次の多項式での近似を行うことによる誤差の増大に起因します。
- degree <= 7
- 最適化パラメータ( param )
誤差の計算式は、n次多項式(1<=n)の式を 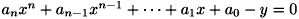 とすると、以下の通りとなります。
とすると、以下の通りとなります。
![\[ \epsilon _{i} = |a_{n}x^{n}_{i} + a_{n-1}x^{n-1}_{i} + \cdots + a_{1}x_{i} + a_{0} - y_{i}| \]](form_1012.png)
F_FIT_MESTIMATOR または、 F_FIT_RANSAC を指定した場合、 param は 誤差 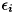 の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
の標準偏差となります。 標準偏差より95%信頼区間内の点をインライアと判定します。 つまり、 [-1.96σ, 1.96σ] より、95%信頼区間が計算されます。 推定した、対象点群の標準偏差をパラメータとして入力してください。
F_FIT_MESTIMATOR2 を指定した場合、param は 誤差 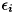 の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
の標準偏差の係数です。 標準偏差は、自動的に計算されます。 F_FIT_MESTIMATOR と F_FIT_RANSAC では、[-1.96σ, 1.96σ] と1.96に固定されていた係数を、自由に指定することができます。 例えば、以下の信頼区間内の点をインライアとして判定したい場合は、次の係数を入力してください。
- 90%信頼区間内:1.645
- 95%信頼区間内:1.960
- 99%信頼区間内:2.567
- 99.9%信頼区間内:3.291
- F_FIT_RANSAC : degree * 5
なお F_FIT_MESTIMATOR、 F_FIT_RANSAC、 F_FIT_MESTIMATOR2 のいずれかを指定した場合、 param に 0 以下の値を指定するとパラメータエラーとなります。
- 乱数
- 引数:
-
[in] pnts 入力点群 [in] pnt_num 入力点群の個数(degree + 1 <= pnt_num) [in] degree 近似したい多項式の次数( 1 <= degree <= 7 ) [in] fitting_mode 近似モード - F_FIT_LSM 最小二乗法
- F_FIT_MESTIMATOR ロバスト推定法(M推定法)
- F_FIT_RANSAC ロバスト推定法(ランザック法)
- F_FIT_MESTIMATOR2 ロバスト推定法(M推定法)…標準偏差を自動決定
[in] param 最適化パラメータ(ロバスト推定法で利用) [out] coefficient 多項式の係数を昇べき順で保持する 要素数は入力degree + 1 に等しい
- 戻り値:
-
F_ERR_NONE 正常終了 F_ERR_INVALID_PARAM 不正なパラメータが入力された F_ERR_CALC_IMPOSSIBLE 計算不可 F_ERR_NOMEMORY メモリ不足 F_ERR_CALC_OVERFLOW オーバーフロー発生により計算不能 F_ERR_NO_LICENCE ライセンスエラー、または未初期化エラー
- 参考文献:
- M. A. Fischler, R. C. Bolles, Random Sample Consensus : A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Commun. ACM, no.24, vol.6, pp.381-395, 1981.
- Rousseeuw P. J, Least Median of Squares Regression, Journal of the American Statistical Association, 79, pp.871-880, 1984.
- David A. Forsyth, Jean Ponce, コンピュータビジョン §15.5, 共立出版, 2007.
- 松山隆司 他, コンピュータビジョン 第3章, 新技術コミュニケーションズ, 1998.
- 金谷健一, これならわかる最適化数学, 共立出版, ISBN 4-320-01786-2.
- 使用例1:
//エラー処理は省略していますので、注意してください #include "fie.h" #include "oal_aloc.h" //メモリ管理 #include <math.h> //数学ライブラリ使用 #define WIDTH 256 //出力画像の幅 #define HEIGHT 256 //出力画像の高さ #define PNTS_NUM 256 //入力点の数 #define DEGREE 3 //近似したい多項式の次数 //処理本体部分 VOID fit_polynomial(VOID) { INT i; //ループ用変数 DOUBLE val[3] ; //画像に描画する際の濃度値 F_RANDDESC r; //擬似乱数列生成用データ UINT seed = 152; //乱数因子(適当な値); DOUBLE random; //乱数 DPNT_T * pnts = NULL; //点列の作成 DPNT_T * pnts_ans = NULL; //近似描画用の点群用 DOUBLE param[DEGREE + 1]; //出力パラメータ用の領域 DOUBLE param2[DEGREE + 1]; //出力パラメータ用の領域 INT ret ; //描画用のルート画像 FHANDLE hdst = NULL; //このサンプルでは、3次多項式 f(x) =0.001 * (x - 60) * (x - 120) * (x - 180) + 100 を近似します //乱数の生成子初期化 fnFIE_mtrand_init(seed, &r); //点列領域確保 pnts = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * PNTS_NUM); pnts_ans = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * PNTS_NUM); //出力画像の領域を確保します カラー表示のため、uc8型 3ch を確保 hdst = fnFIE_img_root_alloc( F_IMG_UC8, 3, WIDTH, HEIGHT ); //出力画像を白色(255)で塗りつぶす fnFIE_img_clear(hdst, 255); //点群描画用の濃度値を設定 入力用点群は黒(0, 0, 0)で描画 val[0] = 0; val[1] = 0; val[2] = 0; //乱数を生成して、入力用の点群を生成する for(i = 0; i < PNTS_NUM; i++ ){ //座標の設定 pnts[i].x = i ; //X座標 pnts[i].y = 0.001 * (i - 60) * (i - 120) * (i - 180) + 100 ; //Y座標 //乱数の生成 random = fnFIE_mtrand_real2(&r); pnts[i].x += 25 * (random - 0.5); //Y座標に乱数を付加 pnts[i].y += 50 * (random - 0.5); //点列を描画する if(0 <= pnts[i].y && pnts[i].y < HEIGHT){ fnFIE_draw_circle(hdst, val, F_DRAW_FILL_IN, pnts[i] , 1); } } // 最小二乗法による近似の推定 fnFIE_fit_polynomial(pnts, PNTS_NUM, DEGREE, F_FIT_LSM, 1.0, param); //取得できた係数から、点群を作成 for(i = 0; i < PNTS_NUM; i++){ pnts_ans[i].x = i; pnts_ans[i].y = param[3] * pow(i, 3) + param[2] * pow(i, 2) + param[1] * pow(i, 1) + param[0]; } //近似した点群で曲線を描く 描画の色は(R,G,B)=(255,0,0)で設定する val[0] = 255; val[1] = 0; val[2] = 0; fnFIE_draw_curve(hdst,val,pnts_ans,PNTS_NUM, F_DRAW_CUBIC_CATMULL_ROM); // M推定法による近似の推定 ret = fnFIE_fit_polynomial(pnts, PNTS_NUM, DEGREE, F_FIT_MESTIMATOR2 , 1.96, param2); //取得できた係数から、点群を作成 for(i = 0; i < PNTS_NUM; i++){ pnts_ans[i].x = i; pnts_ans[i].y = param2[3] * pow(i, 3) + param2[2] * pow(i, 2) + param2[1] * pow(i, 1) + param2[0]; } //近似した点群で曲線を描く 描画の色は(R,G,B)=(0,0,255)で設定する val[0] = 0; val[1] = 0; val[2] = 255; fnFIE_draw_curve(hdst,val,pnts_ans,PNTS_NUM, F_DRAW_CUBIC_CATMULL_ROM); //結果を描画したものを保存する 画像描画のため、y方向が下向きに正であることに注意 fnFIE_save_png("result.png", hdst, -1); //解放処理 fnOAL_free(pnts); fnOAL_free(pnts_ans); fnFIE_free_object(hdst); } INT main(VOID) { //FIEライブラリの初期化コール fnFIE_setup(); //処理実行 fit_polynomial(); //終了処理 fnFIE_teardown(); return (0); }
- 処理結果例:
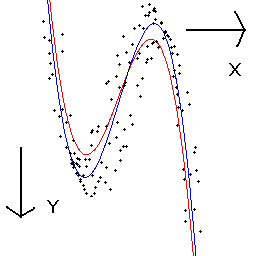
処理結果
- 使用例2:
//エラー処理は省略していますので、注意してください #include "fie.h" #include "oal_aloc.h" //メモリ管理 #include <math.h> //数学ライブラリ使用 #define WIDTH 256 #define HEIGHT 256 #define DEGREE 2 //近似したい多項式の次数 /* このサンプルでは画像の1次元濃度データを、ガウス関数でフィッティングすることを考えます。 ガウス関数G(x)=N exp (-(x - e)^2 / 2σ^2 ) は、G(x)の対数をとることで lnG(x) = lnN + ( -(x - e)^2 / 2σ^2 )という2次関数として見ることができます。 そこで、ガウス関数で近似したいデータ群を2次関数でまず近似し、そこからガウス関数の値を近似します。 */ //処理本体部分 VOID fit_Gaussian(VOID) { INT i; //ループ用変数 DOUBLE val[3] ; //画像に描画する際の濃度値 //入力画像のパラメータ取得用 INT width, height; INT_PTR step; UCHAR * adr; INT pnt_num; //点群の数 DPNT_T * pnts = NULL; //点群を保持する領域 DPNT_T * pnts_ans = NULL; //結果を描画するために使用する領域 DOUBLE param[DEGREE + 1]; //出力パラメータ用の領域 DOUBLE param2[DEGREE + 1]; //出力パラメータ用の領域 DOUBLE N, e, sigma_sqr; //フィッティングするガウス関数のパラメータ FHANDLE hSrc = NULL; //ファイル読み込み用ハンドル FHANDLE hdst = NULL; //描画用のルート画像 //入力画像読み込み //この例では、ガウス分布に従うような濃度分布に、ランダムにノイズが付与されている画像を用います fnFIE_load_img_file("Src1.png",&hSrc, F_COLOR_IMG_TYPE_UC8); //入力画像のパラメータを取得 fnFIE_img_get_params(hSrc, NULL, NULL, &step, &width, &height); adr = (UCHAR *)fnFIE_img_get_adrs(hSrc); //点群領域確保 pnt_num = width; pnts = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * pnt_num); pnts_ans = (DPNT_T*)fnOAL_malloc((sizeof(DPNT_T)) * pnt_num); //出力画像の領域を確保 カラー描画をするので3ch確保 hdst = fnFIE_img_root_alloc( F_IMG_UC8, 3, WIDTH, HEIGHT ); //出力画像を白色(255)で塗りつぶす fnFIE_img_clear(hdst, 255); val[0] = 0; val[1] = 1; val[2] = 2; //ちょうどy座標が中間 横一列の濃度を取得し、対数の値に変換する adr = adr + ( step * ( height / 2)); for(i = 0; i < pnt_num; i++){ pnts[i].x = i; pnts[i].y = adr[i]; //元の濃度の状態はプロットしておく fnFIE_draw_circle(hdst, val, F_DRAW_FILL_IN, pnts[i] , 1); //濃度の値の対数を計算して、点群に設定する if(0 != adr[i]){ pnts[i].y = log(adr[i]); } else{ pnts[i].y = 0; } } // 近似計算を行い近似式を計算する /* 取得できた係数から、ガウス関数を計算する 対数をとって近似した二次多項式の係数と、ガウス関数のパラメータN, e, σ^2には、 二次多項式をf(x) = ax^2 + bx + cとしたときに、次のような関係があります。 N = exp(c - (b^2 / 4a) ) e = -b / 2a σ^2 = -1 / 2a */ // 最小二乗法による近似の推定 fnFIE_fit_polynomial(pnts, pnt_num, DEGREE, F_FIT_LSM, 1.0, param); N = exp(param[0] - ( pow(param[1],2) / (4 * param[2] ) ) ); e = -param[1] / ( 2 * param[2] ); sigma_sqr = -1 / (2 * param[2] ); //取得できた係数から、点群を作成 for(i = 0; i < pnt_num; i++){ pnts_ans[i].x = i; pnts_ans[i].y = N * exp(-pow(i - e, 2) / (2 * sigma_sqr)); } //近似した曲線を描画する 描画色は(R,G,B)=(255,0,0) val[0] = 255; val[1] = 0; val[2] = 0; fnFIE_draw_curve(hdst,val,pnts_ans,pnt_num, F_DRAW_POLYGONAL_LINE); // M推定法による近似の推定 fnFIE_fit_polynomial(pnts, pnt_num, DEGREE, F_FIT_MESTIMATOR2, 1.96 , param2); N = exp(param2[0] - ( pow(param2[1],2) / (4 * param2[2] ) ) ); e = -param2[1] / ( 2 * param2[2] ); sigma_sqr = -1 / (2 * param2[2] ); //取得できた係数から、点群を作成 for(i = 0; i < pnt_num; i++){ pnts_ans[i].x = i; pnts_ans[i].y = N * exp(-pow(i - e, 2) / (2 * sigma_sqr)); } //近似した曲線を描画する 描画色は(R,G,B)=(0,0,255) val[0] = 0; val[1] = 0; val[2] = 255; fnFIE_draw_curve(hdst,val,pnts_ans, pnt_num, F_DRAW_POLYGONAL_LINE); //結果を描画したものを保存する 画像描画のため、y方向が下向きに正であることに注意 fnFIE_save_png("result.png", hdst, -1); //解放処理 fnOAL_free(pnts); fnOAL_free(pnts_ans); fnFIE_free_object(hSrc); fnFIE_free_object(hdst); } INT main(VOID) { //FIEライブラリの初期化コール fnFIE_setup(); //処理実行 fit_Gaussian(); //終了処理 fnFIE_teardown(); return (0); }
- 処理結果例:

入力画像(y=128の横一列の濃度を近似)
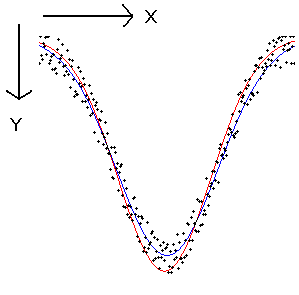
処理結果