特徴量
[総合ドキュメント]

本ページでは、リージョンの特徴量計算と２値ブローブ解析の特徴量計算 で求められる特徴量について説明しています。

area

領域の面積を表す特徴量です。

参照:
fnFIE_region_get_area(), fnFIE_measure_get_area()

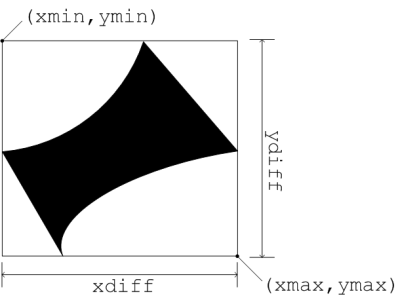
xmin, ymin, xmax, ymax

領域のｘ、ｙ座標の最大値と最小値を表す特徴量です。

blob_xydiff.png

参照:
fnFIE_region_get_xyrange(), fnFIE_measure_get_xyrange()

xmax_at_ymin, xmax_at_ymax, ymin_at_xmax, ymax_at_xmin

領域のｘ、ｙ座標の最大最小位置を表す特徴量です。

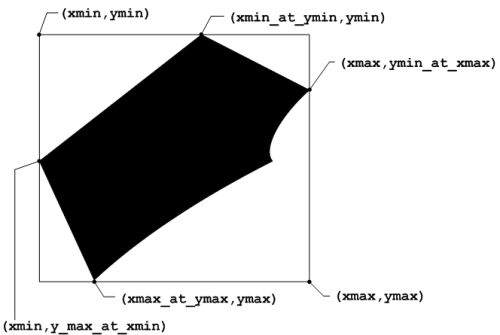
blob_maxminpos.png

参照:
fnFIE_region_get_maxminpos(), fnFIE_measure_get_maxminpos()

xdiff, ydiff

外接矩形の横サイズ(xdiff)と縦サイズ(ydiff)を表す特徴量です。
blob_xydiff.png

下式のように定義されます。

\[{\it xdiff} = xmax - xmin + 1\]

\[{\it ydiff} = ymax - ymin + 1\]

参照:
fnFIE_region_get_xydiff(), fnFIE_measure_get_xydiff()

rect1_area

傾き０の外接長方形の面積を表す特徴量です。 下式のように定義されます。

\[{\it rect1\_area} = {\it xdiff} \times {\it ydiff}\]

参照:
fnFIE_region_get_rect1_area(), fnFIE_measure_get_rect1_area()

rect1_lratio

傾き０の外接長方形の縦横比を表す特徴量です。 下式のように定義されます。

\[{\it rect1\_lratio} = \frac{\it ydiff}{\it xdiff}\]

参照:
fnFIE_region_get_rect1_lratio(), fnFIE_measure_get_rect1_lratio()

rect1_sratio

傾き０の外接長方形の面積比を表す特徴量です。 下式のように定義されます。

\[{\it rect1\_sratio} = \frac{area}{\it rect1\_area}\]

参照:
fnFIE_region_get_rect1_sratio(), fnFIE_measure_get_rect1_sratio()

sumx, sumy

１次モーメントを表す特徴量です 下式のように定義されます。

\[sumx = \sum_{y}\sum_{x}{x} \]

\[sumy = \sum_{y}\sum_{x}{y} \]

より一般化したＮ次モーメントの定義は モーメント を参照してください

参照:
fnFIE_region_get_moment1(), fnFIE_measure_get_moment1()

sumx2, sumy2, sumxy

２次モーメントを表す特徴量です。 下式のように定義されます。

\[sumx2 = \sum_{y}\sum_{x}{x^2} \]

\[sumy2 = \sum_{y}\sum_{x}{y^2} \]

\[sumxy = \sum_{y}\sum_{x}{xy} \]

より一般化したＮ次モーメントの定義は モーメント を参照してください

参照:
fnFIE_region_get_moment2(), fnFIE_measure_get_moment2()

モーメント

モーメントを表す特徴量です。 下式のように定義されます。

\[M_{pq} = \sum_{(x,y) \in R}{x^p y^q} \]

ここで、

なお、p=q=0 のとき、 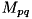$M_{pq}$ は面積と等しく、式で表せば

\[ M_{00} = area \]

となります。

また、sumx, sumy および sumx2, sumy2, sumxy はそれぞれ M の別名称です。それぞれ次のように対応しています。

\[M_{10} = sumx \]

\[M_{01} = sumy \]

\[M_{20} = sumx2 \]

\[M_{02} = sumy2 \]

\[M_{11} = sumxy \]

参照:
fnFIE_region_get_moment1(), fnFIE_measure_get_moment1()

fnFIE_region_get_moment2(), fnFIE_measure_get_moment2()

fnFIE_region_calc_moment3(), fnFIE_measure_get_moment3()

fnFIE_region_calc_moment(), fnFIE_measure_get_moment()

重心モーメント

重心モーメントを表す特徴量です。 下式のように定義されます。

\[MG_{pq} = \sum_{(x,y) \in R}{(x-centerx)^p(y-centery)^q} \]

なお、p+q≦1 のときは次のようになります。

\[ MG_{00} = M_{00} = area \]

\[ MG_{10} = 0 \]

\[ MG_{01} = 0 \]

ここで、

参照:
fnFIE_region_calc_central_moment2(), fnFIE_measure_get_central_moment2()

fnFIE_region_calc_central_moment3(), fnFIE_measure_get_central_moment3()

fnFIE_region_calc_central_moment(), fnFIE_measure_get_central_moment()

Huモーメント不変量

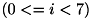領域のHuモーメント不変量を表す特徴量です。 Huモーメント不変量は、正規化された 重心モーメント から算出される、平行移動、 回転、スケール変化に不変な7つの値 $h[i]$ です $(0 <= i < 7)$。 下式のように定義されます。

\[ \begin{aligned} h[0] &= N_{20} + N_{02} \\ h[1] &= (N_{20} - N_{02})^2 + 4 N_{11}^2 \\ h[2] &= (N_{30} - 3 N_{12})^2 + (3 N_{21} - N_{03})^2 \\ h[3] &= (N_{30} + N_{12})^2 + (N_{21} + N_{03})^2 \\ h[4] &= (N_{30} - 3 N_{12})(N_{30} + N_{12}) ((N_{30} + N_{12})^2 - 3(N_{21} + N_{03})^2) + (3 N_{21} - N_{03})(N_{21} + N_{03}) (3(N_{30} + N_{12})^2 - (N_{21} + N_{03})^2) \\ h[5] &= (N_{20} - N_{02}) ((N_{30} + N_{12})^2 - (N_{21} + N_{03})^2) + 4 N_{11}(N_{30} + N_{12})(N_{21} + N_{03}) \\ h[6] &= (3 N_{21} - N_{03})(N_{30} + N_{12}) ((N_{30} + N_{12})^2 - 3(N_{21} + N_{03})^2) - (N_{30} - 3 N_{12})(N_{21} + N_{03}) (3(N_{30} + N_{12})^2 - (N_{21} + N_{03})^2) \\ \end{aligned} \]

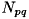ここで $N_{pq}$ は正規化された重心モーメントであり、下式のように定義されます。

\[N_{pq} = \frac{MG_{pq}}{area^{(p+q)/2+1}}\]

正規化された重心モーメントは、平行移動に加えてスケール変化に対しても不変です。

必ずしも高い識別性能が得られるわけではありませんが、Huモーメント不変量は領域の識別に利用することができます。

参考文献:
参照:
fnFIE_region_calc_hu_moments(), fnFIE_measure_get_hu_moments()

centerx, centery

領域の重心を表す特徴量です。 下式のように定義されます。

\[centerx = \frac{sumx}{area}\]

\[centery = \frac{sumy}{area}\]

参照:
fnFIE_region_get_center(), fnFIE_measure_get_center()

majoraxis, minoraxis, axistheta, axisratio

領域の２次モーメントと等価な楕円（慣性等価楕円）を表す特徴量です。 慣性等価楕円の中心は、重心と同じです。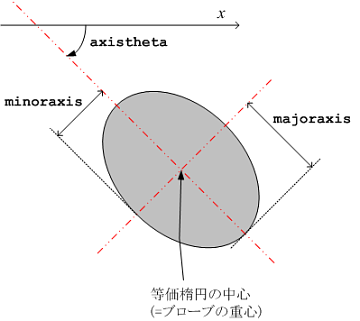
blob_equi_ellipse.png

下式のように定義されます。

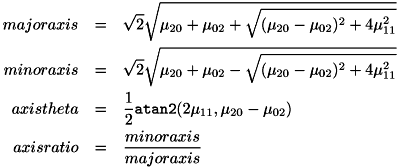
\begin{eqnarray*} majoraxis &=& \sqrt{2}\sqrt{\mu_{20}+\mu_{02}+\sqrt{(\mu_{20}-\mu_{02})^2+4\mu_{11}^2}}\\ minoraxis &=& \sqrt{2}\sqrt{\mu_{20}+\mu_{02}-\sqrt{(\mu_{20}-\mu_{02})^2+4\mu_{11}^2}}\\ axistheta &=& \frac{1}{2}{\tt atan2}(2 \mu_{11},\mu_{20}-\mu_{02})\\ axisratio &=& \frac{minoraxis}{majoraxis} \end{eqnarray*}

但し、axisratio は右辺分母 majoraxis が０の時は０になります。 また、axistheta はラジアンで表され、その角度範囲は 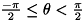$ \frac{-\pi}{2} \le \theta < \frac{\pi}{2} $ です。

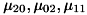ここで、 $\mu_{20}, \mu_{02}, \mu_{11}$ はブローブの 正規化された重心２次モーメントであり、それぞれ次のように計算されます。

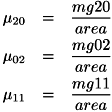
\begin{eqnarray*} \mu_{20} &=& \frac{mg20}{area} \\ \mu_{02} &=& \frac{mg02}{area} \\ \mu_{11} &=& \frac{mg11}{area} \end{eqnarray*}

注意:
ブローブの面積が１（１画素のみブローブ）のときは、majoraxis, minoraxis が共に０になります。 ブローブの構成画素が１直線上に並んでいる場合は、minoraxis が０になります。
参考文献:
Robert M. Haralick and Linda G. Shapio, ``Computer and Robot Vision, Vol.1'' ISBN 0-201-10877-1, Addison-Wesley Publishing Company, 1991, pp.639-

参照:
fnFIE_region_get_equivalent_ellipse(), fnFIE_measure_get_equivalent_ellipse()

diameter_equidisk

領域の面積と等価な円を表す特徴量です。
下式のように定義されます。

\[diameter\_equidisk = 2 \sqrt{ \frac{area}{\pi} }\]

参照:
fnFIE_region_calc_equivalent_disk(), fnFIE_measure_get_equivalent_disk()

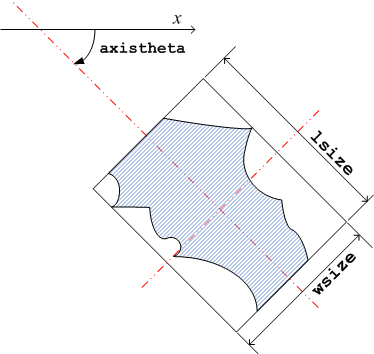
lsize, wsize

慣性主軸と同じ傾きの、領域に外接する長方形のサイズを表す特徴量です。 慣性主軸とは慣性等価楕円の主軸のことで、 axistheta と本ライブラリでは表記しています。 領域内の点(x,y)は(x-0.5,y-0.5),(x+0.5,y-0.5),(x-0.5,y+0.5),(x+0.5,y+0.5)で囲まれる 矩形分の広がりを持っているという定義で外接長方形を求めています。（ feret_diameter 参照 ）

blob_rect2.png

参照:
fnFIE_region_get_rect2_size(), fnFIE_measure_get_rect2_size()

rect2_area

慣性主軸と同じ傾きの、領域に外接する長方形の面積を表す特徴量です。 慣性主軸とは慣性等価楕円の主軸のことで、 axistheta と本ライブラリでは表記しています。

rect2_area は下式にて定義されます。

\[{\it rect2\_area} = wsize \times lsize \]

参照:
fnFIE_region_get_rect2_area(), fnFIE_measure_get_rect2_area()

rect2_lratio

慣性主軸と同じ傾きの、領域に外接する長方形の縦横比を表す特徴量です。 慣性主軸とは慣性等価楕円の主軸のことで、 axistheta と本ライブラリでは表記しています。

rect2_lratio は下式にて定義されます。

\[{\it rect2\_lratio} = \frac{wsize}{lsize}\]

参照:
fnFIE_region_get_rect2_lratio(), fnFIE_measure_get_rect2_lratio()

rect2_sratio

慣性主軸と同じ傾きの領域に外接する長方形の面積比を表す特徴量です。 慣性主軸とは慣性等価楕円の主軸のことで、 axistheta と本ライブラリでは表記しています。

rect2_sratio は下式にて定義されます。

\[{\it rect2\_sratio} = \frac{area}{\it rect2\_area}\]

参照:
fnFIE_region_get_rect2_sratio(), fnFIE_measure_get_rect2_sratio()

feret_diameter

領域の指定角でのフェレ径を表す特徴量です。

フェレ径は、座標点の広がりを考える場合と、考えない場合の２通りの計測モードがあります。 座標点の広がりを考えないモードでは、１点のみの領域はどの角度で計測してもフェレ径の値は0となります。

座標点の広がりを考えるモードでは、領域の面積が１画素以上有る場合、出力のフェレ径の値は1.0以上となります。 （例えば1点のみの領域の場合で角度が0度、または±90度のときに1.0が出力されます。） 領域内の１点は幅１の正方矩形領域であるという定義の下に幅計測します。 例えば、領域上の座標(x,y)の点は、左上(x-0.5,y-0.5)、左下(x-0.5,y+0.5)、右下(x+0.5,y+0.5)、右上(x+0.5,y-0.5)で囲まれる矩形領域とみなします。 この時、1画素のみの領域を45度で計測したフェレ径の値は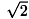$\sqrt{2}$となります。

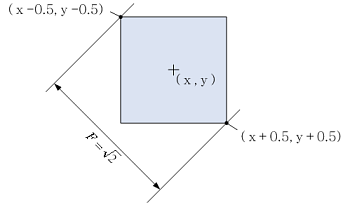
blob_feret_1pix.png

4画素の正方形領域に対して、45度でのフェレ径の、各モードでの例を下図に示します。

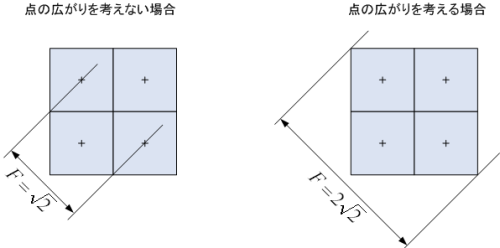
blob_feret_4pix.png

フェレ径（Feret's diameter）とは
フェレ径とは、物体が２本の平行な直線によって挟まれた時の２直線の距離です。 下図のＦは、斜めに傾いた２直線に領域が挟まれた場合の直線間距離ですが、これがフェレ径のイメージです。 同じく下図のFxが水平方向のフェレ径、Fyが垂直方向のフェレ径になります。 なお点の広がりを考えた場合は、Fxはxdiffと、Fyはydiffとそれぞれ等しい値となります。

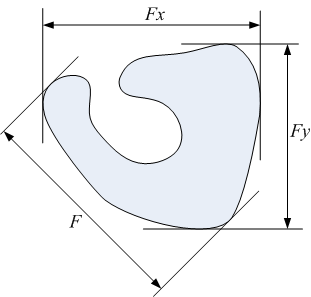
blob_feret1.png

角度について
引数の角度(theta)には幅を計測する軸とＸ軸がなす角度を入力してください。

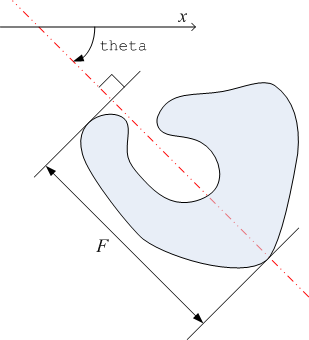
blob_feret2.png

参照:
fnFIE_region_calc_feret_diameter(), fnFIE_measure_get_feret_diameter()

feretmax, feretmin, fmax_theta, fmin_theta

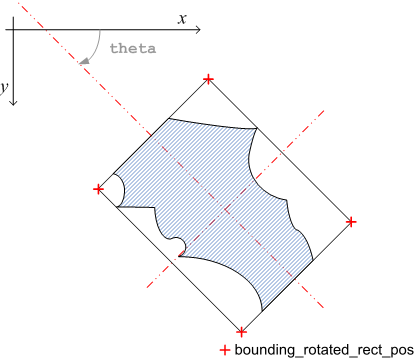
領域の フェレ径 が最大となる計測角度とそのときのフェレ径、 また、最小となる計測角度とそのときのフェレ径です。 角度値(fmax_theta, f_min_theta)はラジアンで、角度範囲は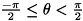 $ \frac{-\pi}{2} \le \theta < \frac{\pi}{2}$ です。 （フェレ径計測角度は+PI回転しても同じなので、この角度範囲となります。）

参照:
fnFIE_region_calc_feret_diameter_maxmin(), fnFIE_measure_get_feret_diameter_maxmin()

凸包

凸包とは、その領域を含む最小の凸多角形のことです。 直感的に言い表すと、木の板に釘を(同じ面に)いくつか打ち付けた後、 その釘がすべて入るように外側から輪ゴムで留めたときにできる輪ゴムの形が凸包となります。 データ解析的には凸多角形という非常に扱い易い形で点集合全体を近似している、と考えられます。

blob_convex2d.png

参照:
fnFIE_region_calc_convex2d(), fnFIE_measure_get_convex2d()

最小外接円

最小外接円（最小包含円とも呼ばれる）とは、 領域外周の点の2点または3点に接する（点を通る）円で、 かつ領域内のすべての点を内包する円のうち最小のものです。

blob_circumcircle.png

最小外接円例

但し、点の広がりについては考慮しません。円と接する点においては、 円はその点の中心を通ります。このため、領域内の点が１点しか無い場合は 最小外接円を求めることは出来ません。

参照:
fnFIE_region_calc_circumcircle(), fnFIE_measure_get_circmcircle()

外接長方形の頂点座標

対象ブローブの外接長方形の４頂点座標です。 座標点列は、0度のときに画像座標系で左上となる点を始点に、 時計回りに頂点を返します。

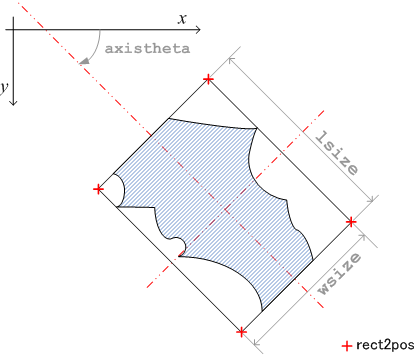
blob_rect2pos.png

参照:
fnFIE_region_calc_rect2pos(), fnFIE_measure_get_rect2pos()

外接長方形の頂点座標（指定角）

対象ブローブの指定した傾きをもった外接長方形の４頂点座標です。 座標点列は、0度のときに画像座標系で左上となる点を始点に、 時計回りに頂点を返します。

blob_bounding_rotated_rect_pos.png

領域内の点(x,y)は(x-0.5,y-0.5),(x+0.5,y-0.5),(x-0.5,y+0.5),(x+0.5,y+0.5)で囲まれる 矩形分の広がりを持っているという定義で指定角の外接長方形を求めています。（ feret_diameter 参照 ）

角度について
引数の角度(theta)には外接長方形のある一辺に平行な軸とＸ軸がなす角度を入力してください。

参照:
fnFIE_region_calc_bounding_rotated_rect_pos(), fnFIE_measure_get_bounding_rotated_rect_pos()

diameter_equicircle

領域の周囲長と円周が等価な円の直径です。

diameter_equicircle は下式にて定義されます。

\[{\it diameter\_equicircle} = \frac{perim}{\pi}\]

参照:
fnFIE_region_calc_equivalent_circle(), fnFIE_measure_get_equivalent_circle()

convex_area, convex_perim

凸包の面積と周囲長を表す特徴量です。 凸包については ここ を参照してください。

参照:
fnFIE_region_calc_convexfeature(), fnFIE_measure_get_convexfeature()

convex_arearatio, convex_perimratio

凸包の面積比(領域の面積/凸包面積)、凸包の周囲長比(領域の周囲長/凸包周囲長)を表す特徴量です。

それぞれ下式にて定義されます。

\[{\it convex\_arearatio} = \frac{\it area}{\it convex\_area}\]

\[{\it convex\_perimratio} = \frac{\it perim}{\it convex\_perim}\]

参照:
fnFIE_region_calc_convexratio(), fnFIE_measure_get_convexratio()

dpmax, dpmin, dpave, dpsigma

領域の重心と境界点列の距離最小値、距離最大値、距離平均値、距離標準偏差値を 表す特徴量です。

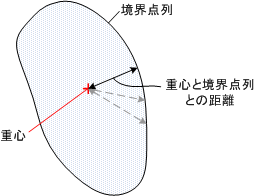
blob_dp.png

参照:
fnFIE_region_get_distance_to_boundary(), fnFIE_measure_get_distance_to_boundary()

circularity1

領域の真円度を表す特徴量です。 circularity1 は下式にて定義されます。

\[circularity1 = 4\pi \frac{area}{perim^2} \]

但し、分母が０（周囲長が０）の時は circularity1 は0.0とします。

参照:
fnFIE_region_calc_circularity1(), fnFIE_measure_get_circularity1()

circularity2

領域の真円度を表す特徴量です。 circularity2 は下式にて定義されます。

\[circularity2 = \frac{area}{\pi * dpmax^2} \]

但し、分母が０（外周距離最大値dpmaxが０）の時は circularity2 は 0.0とします。

参照:
fnFIE_region_calc_circularity2(), fnFIE_measure_get_circularity2()

circularity3

領域の真円度を表す特徴量です。 circularity3 は下式にて定義されます。

\[circularity3 = 1-\frac{dpsigma}{dpave} \]

但し、分母が０（外周距離平均値dpaveが０）の時は circularity3 は 1.0 とします。

参照:
fnFIE_region_calc_circularity3(), fnFIE_measure_get_circularity3()

ns

ブローブの兄弟数を表す特徴量です。 ブローブの親子関係については 親子関係 を参照してください。

参照:
fnFIE_measure_get_sibling_num()

holes

領域の穴の数を表す特徴量です。

参照:
fnFIE_measure_get_hole_num()

sc, st

領域の穴の面積と、穴を含んだ全面積を表す特徴量です。

注意
２値ブローブ解析では、穴はブローブの子供とその子孫を全て含んだ領域 と定義しています。そのため、子供ブローブ面積の総和と穴面積は異なることが 有ることに注意してください。
blob_holes.png

Fig. 穴面積と子供面積が異なる例

参照:
fnFIE_measure_get_hole_area()

hratio

領域の穴面積比を表す特徴量です。 hratioは下式にて定義されます。

\[ hratio = \frac{sc}{st} \]

参照:
fnFIE_measure_get_hole_ratio()

dsmax, dsmin, dsave

兄弟ブローブ間距離を表す特徴量です。 計測対象対象のブローブの重心と、そのブローブの兄弟ブローブの重心との距離を計測します。 ブローブの親子関係については 親子関係 を参照してください。

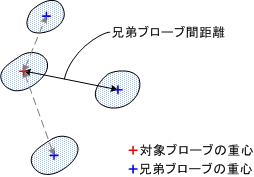
blob_distance_to_siblings.png

参照:
fnFIE_measure_get_distance_to_siblings()

dcmax, dcmin, dcave

子供ブローブ間距離を表す特徴量です。 計測対象のブローブの重心と、そのブローブの子供ブローブの重心との距離を計測します。 ブローブの親子関係については 親子関係 を参照してください。

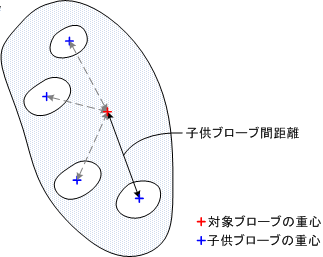
blob_distance_to_childs.png

参照:
fnFIE_measure_get_distance_to_childs()

pps

面積周囲長比を表す特徴量です。 ppsは下式にて定義されます。

\[ pps = \frac{perim^2}{st} \]

参照:
fnFIE_measure_get_pps()

perim

周囲長を表す特徴量です。 ブローブの境界点列のユークリッド距離を周囲長と定義し、その値を計算します。

注意
周囲長は連結性の設定により値が変化します。( feature_boundary の項参照 ) 連結性の設定は、リージョンの場合は fnFIE_region_set_connection() にて、 ブローブ解析の場合は fnFIE_measure_execute() の実行時パラメータにて設定します。 また、ブローブ解析の場合は、前景ブローブの連結性と、背景ブローブの連結性が 逆になりますので注意してください。
参照:
fnFIE_region_get_perimeter(), fnFIE_measure_get_perimeter()

feature_boundary

領域の周囲座標列です。 領域の境界には external boundary と internal boundary の２種類があります。（下図参照）

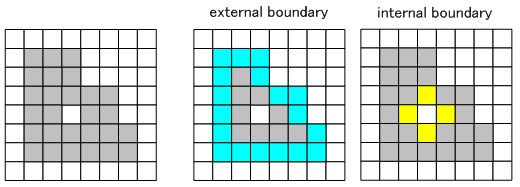
fie_region_boundary_01.png

また、周囲座標は４連結と８連結の場合で座標が異なることがあります。

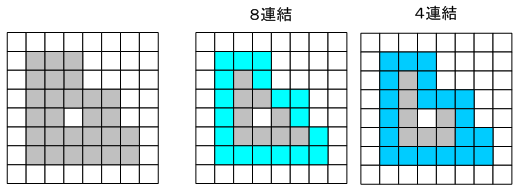
fie_region_boundary_02.png

本ライブラリでは境界座標は、external boundaryは画像座標系で反時計回りに探索（右手の法則）、 internal boundaryは画像座標系で時計回りに探索します。

注意
  • 周囲座標は連結性の設定により値が変化します。
  • 連結性の設定：リージョンの場合は fnFIE_region_set_connection() にて、 ブローブ解析の場合は fnFIE_measure_execute() の実行時パラメータにて設定します。 また、ブローブ解析の場合は、前景ブローブの連結性と、背景ブローブの連結性が 逆になりますので注意してください。
  • FVLなどのFASTの境界点抽出ライブラリとは得られる結果が異なります。
参照:
fnFIE_region_calc_boundary(), fnFIE_measure_get_boundary()

fnFIE_region_calc_boundary_ex(), fnFIE_measure_get_boundary_ex()

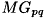Documentation copyright © 2009-2024 FAST Corporation.
Generated on Fri Aug 9 16:38:46 2024 for FIEライブラリ by doxygen 1.5.6-FASTSP-p2